Stechiometrie

Co potřebujeme vědět?

Abychom mohli používat stechiometrii, potřebujeme mít znalosti v řadě oblastí, včetně: rovnic chemických reakcí, stechiometrických koeficientů, molárních a molárních hmotností a molárních objemů plynů a Avogadrova zákona . Pomocí znalostí stechiometrie chemických reakcí lze vyřešit mnoho výpočtových problémů, jako například:

• elementární analýza,
• molární výpočty,
• hmotnostní výpočty,
• výpočet nestechiometrických směsí s možností stanovení limitující látky v reakci,
• reakční výtěžek.

Molární hmotnost

Kvůli nepředstavitelně malé hmotnosti jednotlivých atomů a molekul vznikla jednotka (u) , vyjadřující atomovou hmotnost. V praxi se jedná o hodnotu rovnou 1/12 hmotnosti izotopu uhlíku ¹² C. Tento podíl látky úzce souvisí s Avogadrovou konstantou a je určen jako počet gramů látky, která obsahuje 6,022·10 ²³ atomů, molekul nebo iontů. Molární hmotnost [M] je číselně rovna atomové nebo molekulové hmotnosti a jednotka je g/mol.

Molární objem látky [Vm]

Toto je hodnota specifická pro látku, která silně závisí na teplotě a tlaku. Toto je objem látky, který zabírá jeden její mol. Za normálních podmínek je přijata konstantní hodnota 22,4 dm ³ .

Zákon konstantního složení a zachování hmoty

Každá chemická sloučenina, bez ohledu na její původ a způsob jejího získávání, má dobře definované a konstantní kvalitativní a kvantitativní složení. Oxid sírový (IV) například vždy obsahuje 50 %hmotn. síry a oxid sírový (VI) 40 %hmotn. tohoto prvku. V uzavřeném systému se hmotnost výsledných produktů rovná hmotnosti substrátů spotřebovaných během reakce. Zákon zachování hmotnosti se odráží v potřebě vyrovnat každou rovnici chemické reakce příslušnými chemickými koeficienty tak, aby se obě strany rovnice rovnaly počtu přítomných atomů. Stechiometrické poměry odrážejí molární poměry reaktantů přítomných v chemické reakci.

Chemická reakční rovnice

Všechny potřebné informace o relativních vztazích mezi chemickými látkami jsou odvozeny z rovnice jejich chemické reakce. Poskytuje některé důležité relativní a kvantitativní informace.

Příklad 1

Z rovnice pro syntézu amoniaku , která následuje po reakci: můžeme provést několik interpretací – molekulové, molární, molární hmotnosti, molární objemy a molekulová čísla. a) Molekulárně můžeme vyčíst, že tři molekuly vodíku reagují s jednou molekulou dusíku za vzniku dvou molekul amoniaku. b) To také znamená, že tři moly vodíku reagují s jedním molem dusíku za vzniku produktu dvou molů amoniaku. c) Pomocí periodické tabulky chemických prvků , která obsahuje molární hmotnosti jednotlivých atomů, můžeme z rovnice také usoudit, že 6 g vodíku zcela zreagovalo s 28 g dusíku za vzniku 34 g amoniaku. d) Pak za normálních podmínek víme, že jeden mol plynu zabírá 22,4 dm ³ . To nám umožňuje dojít k závěru, že 67,2 dm ³ vodíku reaguje s 22,4 dm ³ dusíku za vzniku 44,8 dm ³ amoniaku. e) Dalším užitečným vztahem je Avogadrův zákon, který říká, že stejné objemy různých plynů obsahují stejný počet částic za stejných podmínek tlaku a teploty. Když známe Avogadrovu konstantu 6,022· ¹⁰²³ _, víme, že potřebujeme 3·6,022· ¹⁰²³ molekul vodíku a 6,022· ¹⁰²³ molekul dusíku k provedení kompletní chemické reakce pro syntézu amoniaku. Reakce poskytuje 2·6,022· ¹⁰²³ molekul amoniaku.

Příklad 2

Spalovací reakce hořčíku v chlóru probíhá podle rovnice: nám umožňuje přijít s interpretacemi podobnými předchozímu příkladu. a) I na první pohled nám uvedená rovnice umožňuje dojít k závěru, že abychom získali jednu molekulu chloridu hořečnatého , musíme jako substráty dodat jednu molekulu hořčíku a jednu molekulu chloru. b) To je samozřejmě ekvivalentní počtu molů přítomných v systému, tj. jeden mol hořčíku, jeden mol chloru, jeden mol chloridu hořečnatého. c) Pro hmotnostní výpočty víme, že 24 g hořčíku reaguje se 71 g chloru za vzniku 95 g chloridu hořečnatého. d) Protože se uvažované chemické reakce účastní pouze jeden plyn, chlor , můžeme pro něj také napsat, že zaujímá objem 22,4 dm ³ . e) V počtech částic je každá složka rovna druhé a má hodnotu 6,022·10 ²³ .

Procentuální výtěžek chemické reakce [ %W]

Stechiometrické výpočty se také používají ke zjištění výtěžku reakce, tj. poměru skutečného množství získaného produktu k množství odvozenému z rovnice chemické reakce.

Příklad 1

Byla provedena oxidační reakce 30 kg oxidu siřičitého a v přítomnosti platinového katalyzátoru bylo získaným produktem 34 kg oxidu siřičitého. S jakým byl výnos tohoto procesu? Rovnice chemické reakce: Ze zaznamenané reakce můžeme vidět, že dva moly oxidu siřičitého produkují stejné množství molů oxidu siřičitého. Když známe molární hmotnosti reaktantů, víme, že stechiometricky, za předpokladu 100%výtěžku, 128 g SO ₂ produkuje 160 g SO ₃ . S těmito znalostmi můžeme uspořádat poměr: 0,128 kg SO ₂ – 0,160 kg SO ₃ 30 kg SO ₂ – x kg SO ₃ Odtud zjistíme množství oxidu siřičitého, které by vzniklo na 100 procent. výtěžek. 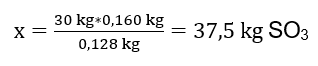Při znalosti teoretického a skutečného množství SO ₃ můžeme vypočítat výtěžek, při kterém k reakci došlo. 37,5 kg SO ₃ – 100%výtěžnost 34 kg SO ₃ – x%výtěžnost 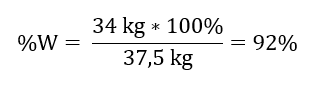Oxidace oxidu siřičitého na oxid siřičitý za použití platinového katalyzátoru proběhla s 92%výtěžkem.

Molekulární a elementární vzorce

Další aplikací stechiometrických výpočtů je stanovení vzorců jednoduchých chemických sloučenin. Molekulární vzorec chemické sloučeniny je shodný s empirickým vzorcem nebo je jeho celočíselným násobkem. Pokud víme, že obecný vzorec chemické sloučeniny je N _x O _y , lze hodnoty stechiometrických indexů vypočítat vydělením hmotnosti na atomy jejich atomovými hmotnostmi. Pokud není známa molekulová hmotnost chemické sloučeniny, ale pouze její procentuální složení, lze uvést pouze elementární vzorec. Může to být věrné zobrazení molekulárního vzorce nebo pouze určení poměru jednotlivých prvků.

Příklad 1

Molekulová hmotnost chemické sloučeniny je 92 u a skládá se z 30,43 %dusíku a 69,57 %kyslíku. Jaký je molekulární vzorec chemické sloučeniny? Protože součet molekul přítomných ve sloučenině je 100 %, můžeme předpokládat, že: 92 u – 100 %To nám umožňuje vypočítat jednotlivé obsahy prvků: 92 u – 100 %xu dusíku – 30,43 %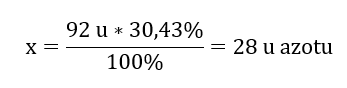 Víme tedy, že hmotnost na atom kyslíku je: 92 u – 28 u = 64 u Při znalosti jednotlivých hmotností prvků můžeme určit stechiometrické indexy: 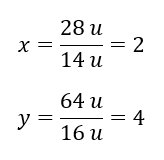Molekulární vzorec této chemické sloučeniny je N ₂ O ₄ .

Příklad 2

V chemické sloučenině jsou dva prvky – kyslík se 60 %a síra 40 %. Jaký je jeho elementární vzorec? Obecný vzorec je S _x O _y , kde x je 40 %a y je 60 %. Když známe molární hmotnosti jednotlivých prvků, lze to znázornit takto: 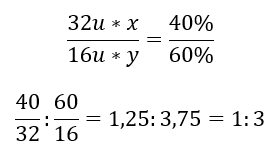To znamená, že v dané chemické sloučenině připadají na každý atom síry tři atomy kyslíku. Elementární vzorec je SO ₃ .

Přebytečný a omezující substrát

V případě reakcí, ve kterých jsou reaktanty přítomny v poměrech odlišných od jejich odpovídající stechiometrie, jeden z reaktantů zcela zreaguje a reakce se zastaví. Poté je přítomen ve formě omezujícího reaktantu, zatímco druhý reaktant bude v systému v přebytku a bude také stále přítomen v systému ve své primární formě, když je reakce dokončena.

Příklad 1

V laboratoři reagovalo 40 cm ³ 0,25 M roztoku síranu hlinitého s 50 cm ³ 0,5 M roztoku chloridu barnatého. Kolik gramů sraženiny se vytvoří? Rovnice chemické reakce: Prvním krokem k poznání skutečného průběhu reakce je určení skutečného počtu molů látek účastnících se reakce. n _Al2(SO4)2 : C _Al2(SO4)2 · V _Al2(SO4)2 = 0,25 · 0,04 dm ³ = 0,010 mol n _BaCl2 : C _BaCl2 · V _BaCl2 = 0,5 · 0,05 dm ³ = 0,025 mol Druhým krokem je ke stanovení deficitního substrátu na základě stechiometrie reakce – tím se určí množství vytvořené sraženiny. 1mol Al ₂ (SO ₄ ) ₃ – 3 mol BaCl ₂ 0,010 mol Al ₂ (SO ₄ ) ₃ – x mol BaCl ₂ 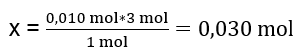K úplnému provedení reakce s 0,010 mol Al ₂ (SO ₄ ) ₃ je nutné přidat 0,030 mol BaCl ₂ do systému. Zreaguje však pouze 0,025 mol chloridu barnatého, což znamená, že je v deficitu a omezí reakci. Proto by se množství sraženiny vytvořené při reakci mělo vypočítat z množství tohoto substrátu. Počet molů použitého chloridu barnatého podle stechiometrie reakce se rovná počtu molů vzniklé sraženiny, tedy: n _BaSO4 = n _BaCl2 0,025 mol BaSO ₄ = 0,025 mol BaCl ₂ Znát počet molů barya síranu, můžeme vypočítat jeho hmotnost: m _BaSO4 = n _BaSO4 · M _BaSO4 m _BaSO4 = 0,025mol · 233,393 g/mol = 5,835 g Reakcemi a množstvími substrátů uvedenými v úloze vznikne 5,835 g sraženiny síranu barnatého.