Energetik der chemischen Reaktionen

System und Umgebung der chemischen Reaktion

Für die korrekte energetische Interpretation chemischer Reaktionen ist folgendes Wissen unerlässlich:

1. System – ein abgegrenzter Bereich der Materie, das seine eigenen Grenzen hat. Die Art des Systems ist wichtig: offen, wenn Energie und Materie während der Reaktion ausgetauscht werden, geschlossen, wenn nur Energie ausgetauscht wird, und isoliert, wenn weder Energie noch Materie ausgetauscht werden.
2. Umgebung – alles, was nicht zum System gehört, sich aber in dessen Nähe befindet.
3. Komponenten des Systems – alle Substanzen, die sich in dem betrachteten System befinden und ihre eigenen charakteristischen chemischen Eigenschaften haben.

Energetik der chemischen Bindungen

Der energetische Effekt, der jede chemische Reaktion kennzeichnet, ist das Ergebnis von Veränderungen, die beim Brechen und Bilden von Bindungen zwischen Atomen auftreten. Das Aufbrechen einer chemischen Bindung ist nämlich eng mit der Aufnahme einer entsprechenden Energiemenge verbunden, während die Bildung einer neuen Bindung zu deren Freisetzung führt. Die Abgabe von Energie an die Umwelt kann mit unterschiedlichen Wirkungen erfolgen – in Form von Wärme, Licht, Arbeit oder Strom. Jeder dieser Prozesse ist eine Komponente, die sich auf die Gesamtänderung der inneren Energie des Systems auswirkt, in dem die betrachtete Reaktion abläuft.  Wichtig ist, dass unabhängig davon, ob die Reaktanten bei einer Umwandlung Energie aufnehmen oder abgeben müssen, immer eine bestimmte Menge an Energie erforderlich ist, um den gesamten Prozess in Gang zu setzen.

Erster Hauptsatz der Thermodynamik

Die erste wichtige Regel in Bezug auf die Energetik chemischer Reaktionen ist, formuliert im ersten Hauptsatz der Thermodynamik, die Beziehung, dass die innere Energie eines Systems, das nur Energie mit seiner Umgebung austauscht (ein geschlossenes System), nur in Form von Arbeit und Wärme verändert werden kann.  Dies spiegelt sich in der Helmholtz-Gleichung wider:

∆U = Q + W

Wo ΔU die Änderung der inneren Energie darstellt, Q die Wärme ist und W die Arbeit symbolisiert. Aus dieser Formel geht hervor, dass die innere Energie eines isolierten Systems, d.h. eines Systems, das weder Energie noch Masse mit seiner Umgebung austauscht, konstant ist.

Die Komponenten der inneren Energie hingegen sind alle kinetischen Energien der im Reaktionssystem vorhandenen Atome, Ionen, Moleküle, Elektronen und Atomkernbestandteile sowie die Energien ihrer Wechselwirkungen untereinander, d.h. die Energien der chemischen Bindungen, der Wechselwirkungen zwischen Ladungen und ähnliche. Man beachte, dass die interne Energie nicht die kinetische oder potenzielle Energie des Systems als Ganzes umfasst. Die Summe der kinetischen und potentiellen Energie des gesamten Systems und der inneren Energie ist die Gesamtenergie des Systems (E).

Enthalpie des Systems (H)

Dies ist ein weiterer wichtiger Begriff, der mit der Energetik chemischer Reaktionen zusammenhängt und in der Praxis die Summe aus der inneren Energie des Systems und dem Produkt aus Druck und Volumen bedeutet.  Quantitativ stellt er die Energie dar, die erforderlich ist, um ein System in einem Vakuum (U) zu erzeugen, plus die Arbeit, d.h. den Druck-Volumen-Quotienten (pV), den das System gegen äußere Kräfte leisten muss, um ein von Null verschiedenes Volumen zu erzeugen.  Die Relation, die die Enthalpie eines Systems beschreibt, wird wie folgt ausgedrückt:

H = U + pV

Die Reaktion in einem solchen System führt zu einer unendlich kleinen Änderung der Enthalpie:

dH = dU + dpV + pdV

Für den Fall, dass die Reaktionsbedingungen isobar sind, d.h. sich der Druck während des Prozesses nicht ändert, kann der zweite Glied vernachlässigt werden, da dpV=0 ist.  Nach der Substitution der Differentiale in die endlichen Inkremente und der Umrechnung des Ausdrucks, der sich auf die Änderung der inneren Energie des Systems bezieht, erhalten wir die Relation:

∆H = Q + W + p∆V

Unter der Annahme, dass der betrachtete Prozess volumetrische Arbeit verrichtet, während der Druck stabil bleibt, ist W = -pΔV, und folglich:

∆H = Q – p∆V + p∆V

Aus der Gleichung lässt sich ableiten, dass die Enthalpieänderung dieses Systems gleich der Wärme ist, wenn die Reaktion bei konstantem Druck abläuft:

∆H = Q

Energiepotenzial der Reaktion

Aufgrund der oben abgeleiteten Formel, die beweist, dass die Enthalpieänderung eines Systems gleich der Reaktionswärme sein kann, gibt es eine Einteilung der Prozesse je nach den thermischen Umwandlungen.  Nach der Richtung des Energieflusses werden chemische Reaktionen in folgende Kategorien eingeteilt:

1. Exotherme Reaktionen, d.h. solche, bei denen eine Abgabe von Energie, z.B. in Form von Wärme, an die Umgebung des Systems zu beobachten ist. Dies ist der Fall, wenn die Summe der Enthalpien der Produkte kleiner ist als die Summe der Enthalpien der Substrate, also wenn ΔH<0.
2. Endotherme Reaktionen, also chemische Umwandlungen, die zur Aufnahme von Energie aus der Umgebung führen. Voraussetzung für das Zustandekommen der Reaktion ist, dass diese Energie in ausreichender Menge zugeführt wird. Dies gilt für alle Umwandlungen, bei denen die gesamte Enthalpie der Produkte höher ist als die gesamte Enthalpie der Substrate, d.h. ΔH>0.

Aufzeichnungen der thermochemischen Reaktionen

Bei der Betrachtung chemischer Reaktionen einschließlich ihres Energiebedarfs und ihrer Energieverteilung werden die dafür charakteristischen Wärmeeffekte in die Notation der chemischen Gleichung aufgenommen.  Bei exothermen Reaktionen wird der absolute Wert der auftretenden Energiewirkung auf der Produktseite angegeben. Im Gegensatz dazu wird bei der Aufzeichnung einer endothermen Reaktion der absolute Wert der absorbierten Energie auf der Substratseite aufgezeichnet. Zum Beispiel:

1. Exotherme Reaktion:
   
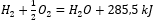
2. Endotherme Reaktion: 2H₃PO₄ + 3Mg(OH)₂ + 407kJ = Mg₃(PO₄)₂ + 6H₂O

Eine andere Möglichkeit ist die Aufzeichnung der Gleichung einer chemischen Reaktion zusammen mit daneben stehendem Wert der Energiewirkung. In diesem Fall ist der Wert, der der Energie einer exoenergetischen Reaktion entspricht, negativ, während der einer endoenergetischen Reaktion positiv ist. Zum Beispiel:

1. Exoenergetischen Reaktion: Fe + S → FeS ∆H= -95,2 kJ/mol
2. Endoenergetischen Reaktion: FeS → Fe + S ∆H= 95,2 kJ/mol

Hessscher Wärmesatz

Er bildet die Grundlage für thermochemische Berechnungen und besagt, dass die thermische Wirkung einer Reaktion unabhängig davon, wie sie durchgeführt wird, immer gleich ist. Dies ermöglicht die Berechnung der standardmäßigen Reaktionsenthalpie (ΔrH^ϴ) unter Annahme der verwendeten Standardbedingungen, d.h. eines Drucks von 10⁵ Pa und einer beliebigen Temperatur. Da die Enthalpie eine Funktion des Zustands ist, hängt ihre Variabilität nur von zwei Werten ab: dem Ausgangszustand und dem Endzustand, was bei der chemischen Reaktion den Zustand der Substrate bzw. der Produkte angibt.  Der Hesssche Wärmesatz drückt sich in einer Gleichung aus, die die stöchiometrischen Koeffizienten (v) und die molaren Standardbildungsenthalpien (ΔfH^ϴ) enthält:

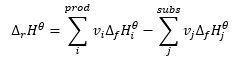
Molare Standardbildungsenthalpie

Dies ist die Enthalpie, die sich aus der Bildung von 1 Mol einer gegebenen chemischen Verbindung aus Elementen in ihrem Grundzustand ergibt.  Dabei wird der Grundzustand als die stabilste Variante des Elements unter den gegebenen Bedingungen betrachtet.  Zum Beispiel ist Graphit bei einer Temperatur von 25^oC und einem Druck von 10⁵ Pa die stabilste Variante von Kohlenstoff.  Bei hohen Temperaturen und hohem Druck hingegen ist seine stabile Form Diamant.

Für jeden Reaktanten, der an der Reaktion im Grundzustand beteiligt ist, ist der Wert der molaren Standardbildungsenthalpie gleich Null. Meistens handelt es sich dabei um einzelne Atome von Edelgasen oder um die unter den gegebenen Bedingungen stabilsten Varianten anderer Gase. Für einen Standarddruck (10⁵ Pa) und eine Standardtemperatur, in der Regel 25^oC, werden die Werte der molaren Standardbildungsenthalpien von Verbindungen in chemischen Tabellen zusammengefasst. Die Einheit dieses Wertes ist .  Die Anwendung des Hessschen Wärmesatzes in chemische Reaktionen führt zu der Tatsache, dass der Enthalpiewert einer Reaktion unabhängig von der Anzahl der Zwischenreaktionen ist. Entscheidend ist nur, dass aus bestimmten Substraten konkrete Produkte gebildet werden.

Synthese von Kohlendioxid

Der Prozess der Synthese von Kohlendioxid kann auf verschiedene Arten durchgeführt werden, aber nach dem Hessschen Wärmesatz führt jede zu demselben Wert der Änderungen der Standardenthalpie.

1. Direkte Synthese
   
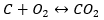
2. Synthese von Kohlenstoff(II)-oxid + Oxidation der Verbindung zu Kohlenstoff(IV)-oxid
   

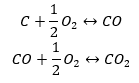
Liest man die Werte der Standardenthalpien für die Bildung von Verbindungen aus der Tabelle ab und setzt sie in die chemischen Gleichungen ein, so ergibt sich für jede Methode die gleiche Enthalpie, nämlich -393,5 kJ/mol.

Kirchhoffsches Gesetz

Es ermöglicht Transformation von Berechnungen zur Errechnung der Standardenthalpie einer Reaktion für eine bestimmte Temperatur, wenn ihr Wert bei einer anderen Temperatur bekannt ist. Die Temperaturabhängigkeit der molaren Wärme aller Reaktanten ist ebenfalls bekannt.  Das Gesetz ist anwendbar, weil die Änderung der Enthalpie einer Reaktion von den Bedingungen abhängt, unter denen sie bestimmt wird – sie variiert bei unterschiedlichen Temperaturen und Drücken. Die Herleitung der Formel muss mit der Definition der Wärmekapazität beginnen, d.h. dem Verhältnis zwischen der zugeführten Wärme und der Temperaturerhöhung:

Unter der Annahme isothermer Bedingungen kann es wie folgt umgewandelt werden:

Die Integralgleichung der sich ergebenden Gleichung und die Umwandlung der Wärmekapazität in einen Glied, der der Änderung der Standardwärmekapazität entspricht, ergibt die Gleichung des Kirchhoffschen Gesetzes:

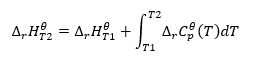
Für Standardbedingungen wird die Änderung der Wärmekapazität einer Reaktion durch eine Gleichung mit den Variablen v, den stöchiometrischen Koeffizienten, und , der molaren Standardwärme eines bestimmten Reaktanten, beschrieben. Bei kleinen Temperaturunterschieden (bis zu 100 K) wird der Wert der molaren Standardwärme des Reaktanten in einem bestimmten Bereich als konstant angenommen. Es ist dann möglich, eine vereinfachte Form des Kirchhoffschen Gesetzes zu verwenden, unter der Annahme, dass die Wärmekapazitäten der Reaktanten nicht von der Temperatur abhängen, und unter konstantem Druck,: