Stoffmengenkonzentration in Lösungen

Angabe der Zusammensetzung der Lösung

Das wichtigste Merkmal jeder Lösung ist die Bestimmung ihrer Zusammensetzung. Die Fertigkeit, die Zusammensetzung einer Lösung zu bestimmen und sie in die gewünschten Einheiten umzurechnen, ist eine grundlegende Fertigkeit für jeden Chemiker. Die Menge eines bestimmten Bestandteils in einem Gemisch kann auf verschiedene Weise definiert werden, z.B. durch die Masse, das Volumen oder die Molarität. Aus diesem Grund gibt es auch verschiedene Arten von Konzentrationen, die die Abhängigkeit der Menge eines Bestandteils von der Menge einer Lösung oder eines Gemischs darstellen. Bei der Beschreibung der Zusammensetzung von Lösungen werden am häufigsten die Begriffe Massenanteil, Volumenanteil, Molenanteil und Stoffmengenkonzentration verwendet. Anteile geben an, welchen Anteil der betreffende Bestandteil an einem bestimmten Gemisch hat. Sie können in Einheiten von Masse, Volumen oder in Mol einer Verbindung ausgedrückt werden.

Stoffmengenkonzentration

Sie ist die am häufigsten gewählte Konzentration, da sie sich am einfachsten handhaben lässt, indem man die Anzahl der Mole eines Stoffes in einem Lösungsvolumen bestimmt. Die theoretische Grundlage ist die Feststellung, dass Lösungen von zwei verschiedenen Substanzen, die die gleiche Konzentration und das gleiche Volumen haben, bei gleicher Temperatur die gleiche Anzahl von Molen und damit auch die gleiche Anzahl von Molekülen der gelösten Substanz enthalten. Dank dieser Abhängigkeit ist es möglich, für Lösungen gleicher Stoffmengenkonzentration das richtige, durch die stöchiometrischen Koeffizienten bestimmte Molverhältnis zu erreichen, indem man das entsprechende Volumen der Lösungen mischt. Das bedeutet, dass bei einer Reaktion des Typs A + B→  C, bei der ein Mol des Stoffes A mit einem Mol des Stoffes B reagiert, die beiden Lösungen mit der gleichen Stoffmengenkonzentration zu gleichen Teilen gemischt werden müssen, damit die Reaktion vollständig abläuft.  Wenn es eine Reaktion vom Typ A + 2B → C ist, d.h. ein Mol der Substanz A reagiert mit zwei Molen der Substanz B, müsste man ein Volumen der Lösung A mit zwei Volumen der Lösung B mischen. In diesem Fall gibt es auch eine andere Lösung, denn statt gleichvolumige Lösungen im Volumenverhältnis 1:2 zu verwenden, kann man ein Volumen der Lösung A und ein Volumen der Lösung B mit der doppelten Konzentration verwenden. Die Stoffmengenkonzentration, die mit dem Symbol C_m bezeichnet wird, gibt die Anzahl der Mole einer Substanz an, die in einer Volumeneinheit enthalten sind, meist in 1 dm³ Lösung.

Die Formel zur Berechnung der Stoffmengenkonzentration ist die Anzahl der Mole des Stoffes (n_s) geteilt durch das Gesamtvolumen der Lösung (V_Los), ausgedrückt in dm³:
C_m=n_s/V_Los

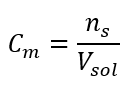
Bei Verwendung der SI-Grundeinheit des Volumens, des Kubikmeters, muss die Mengeneinheit einer Substanz in Kilomol ausgedrückt werden. Dies wirft jedoch keine größeren Rechenprobleme auf, da .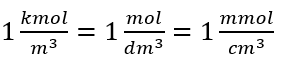

Die Einheit der Stoffmengenkonzentration C_m ist Mol pro Kubikdezimeter, die vereinfacht oft mit dem Symbol M geschrieben wird.

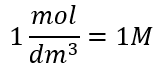
Verwendung der Stoffmengenkonzentration

a) Berechnung der Stoffmengenkonzentration auf der Grundlage des Gehalts eines Bestandteils in Lösung.

Beispiel 1: Die Lösung enthält 30 g Kaliumhydroxid in 3,0 dm³ der Lösung. Berechnen Sie seine Stoffmengenkonzentration.

Schritt 1. Berechnung der molaren Masse KOH

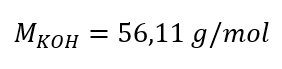
Schritt 2. Berechnung der Anzahl der in der Lösung vorhandenen Mole von KOH

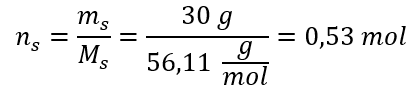
Schritt 3. Berechnung der Stoffmengenkonzentration mit Hilfe der Formel
C_m=n_s/V_Los =(0,53 mol)/(3,0 dm³)=0,18 mol/dm³

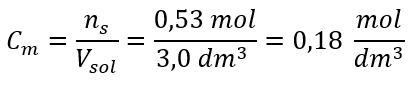
Antwort: Eine Kaliumhydroxidlösung, die 30 g der Substanz in 3,0 dm3 Lösung enthält, hat die Stoffmengenkonzentration C_m =

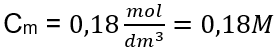
b) Herstellung einer Lösung mit einer bestimmten Konzentration

Beispiel 2. Beispiel 2. Berechnen der Masse der Glucose mit der Formel C₆H₁₂O₆ die erforderlich ist, um 300 cm3 mit der Konzentration von 0,32  herzustellen.

Schritt 1. Berechnung der molaren Masse von Glukose

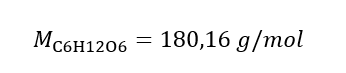
Schritt 2. Berechnung der erforderlichen Masse an Glukose unter Verwendung der umgewandelten Formel für die Stoffmengenkonzentration, wissend, dass :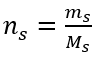

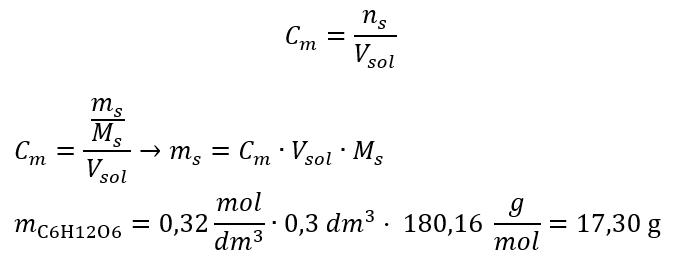
Dank der Berechnung wissen wir, dass zur Herstellung einer solchen Lösung 17,30 g Glukose abgewogen und quantitativ in einen 300 cm³ Messkolben übertragen werden müssen.

Antwort: Zur Herstellung von 300 cm³ Glukoselösung mit der Stoffmengenkonzentration
0,32 müssen 17,30 g des Stoffes abgewogen werden.

c) Verdünnung und Konzentration konzentrierter Lösungen

Mit der Stoffmengenkonzentration kann man auch eine Lösung mit einer vorgegebenen Konzentration (C_m2) herstellen, indem man die konzentrierte Lösung (C_m1) verdünnt, wo:

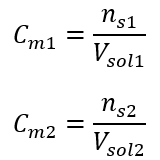
Bei der Verdünnung ändert sich nur das Volumen der Lösung, die Anzahl der Mole der gelösten Substanz bleibt gleich. Es kann daher angenommen werden, dass:

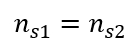
Durch Umformung der Formel für die Stoffmengenkonzentration erhalten wir die Beziehungen:

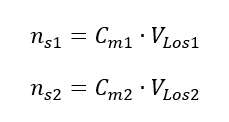
Wissend, dass  bekommen wir eine Gleichung:

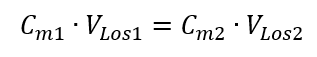
Die Formel für die Verdünnung von Lösungen unter Berücksichtigung der Stoffmengenkonzentration, darunter die neu gewonnene (C_mx) kann daher wie folgt geschrieben werden:

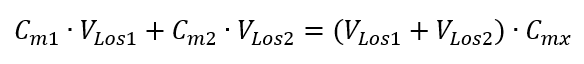
Beispiel 3. Welches Volumen von 0,150 Säure erhält man, wenn man 250 cm³ einer 0,750 mol/dm³ Lösung dieser Säure mit Wasser verdünnt?

Schritt 1. Umformung der Formel unter der Annahme, dass die Wasserkonzentration beträgt = 0 mol/dm³

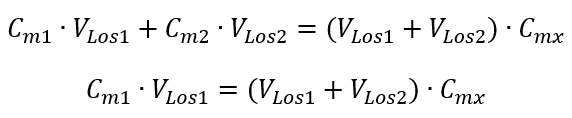
Schritt 2. Berechnung des Gesamtvolumens (V_x)

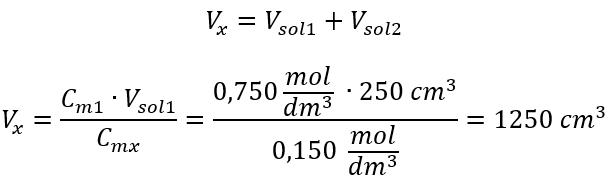
Alternativ kann auch die Abhängigkeit von der Konstanz der Molzahl bei der Verdünnung verwendet werden:

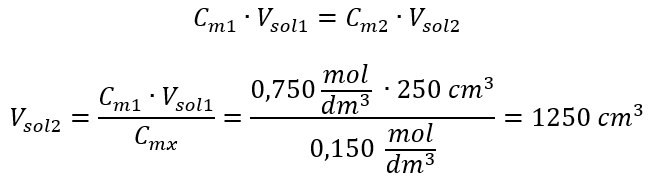
Antwort: Um die Säure auf die gewünschte Konzentration zu verdünnen, muss man 1,25 dm³ Wasser verwenden.

Beispiel 4. Berechnen Sie, wie viel Wasser aus 300 cm³ einer Lösung mit Konzentration von 0,125 mol/dm³, verdampft werden muss, um eine Lösung mit Konzentration von 1,50 mol/dm³ zu erhalten.

Schritt 1. Umformung der Formel für die Änderung der Stoffmengenkonzentration unter der Annahme, dass die Stoffmengenkonzentration von Wasser C_m2 = 0 mol/dm³.

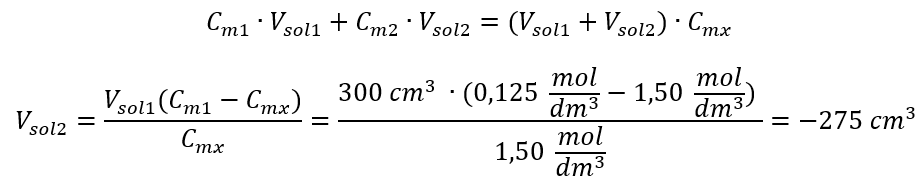
Antwort. Um die Lösung zu konzentrieren, muss man 275  verdampfen.

Umrechnung der Stoffmengenkonzentration gegenüber der prozentualen Konzentration

In der täglichen Laborarbeit ist es notwendig, verschiedene Konzentrationen von Lösungen umzurechnen. Stoffmengenkonzentration und Prozentangaben sind die am häufigsten verwendeten. Es ist möglich, zwischen ihnen zu wechseln, indem man die Dichte der Lösung verwendet. Es ist notwendig, sie in die Formeln für die Konzentrationen von Interesse einzuführen:

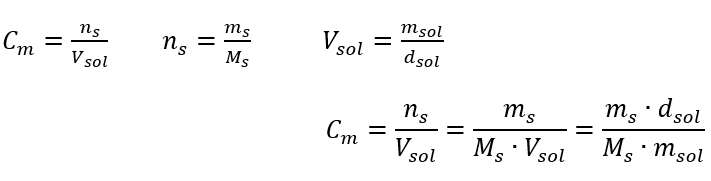
In der Umwandlung ist das Verhältnis zwischen der Masse des Stoffes und der Masse der Lösung zu sehen, das die Grundlage für die prozentuale Konzentration bildet, die durch die folgende Formel ausgedrückt wird:

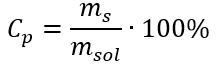
Setzt man die Formel für die prozentuale Konzentration in die zuvor umgewandelte Formel für die Stoffmengenkonzentration ein, erhält man eine Beziehung, die es erlaubt, sich frei zwischen den beiden zu bewegen:

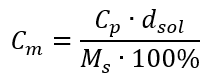
Die einzige Einschränkung der Formel ist die Verwendung der entsprechenden Einheiten, so dass es empfehlenswert ist, diese bei der Berechnung jedes Mal zu berücksichtigen.

Beispiel 5. Berechnen Sie die Stoffmengenkonzentration von Schwefel(VI)säure wissend, dass die prozentuale Konzentration C_p = 98,0%, und die Dichte d = 1,84 kg/dm³ beträgt.

Die Aufgabe kann mit Hilfe von zwei Methoden berechnet werden:

Methode 1 In mehreren Schritten, ohne Verwendung der Formel

Schritt 1. Berechnung der Masse von 1,00 dm³ Säure

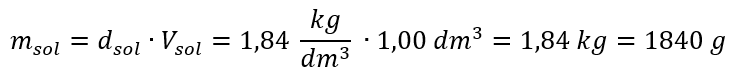
Schritt 2. Berechnung der Masse der Säure unter Berücksichtigung der prozentualen Konzentration

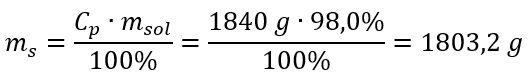
Schritt 3. Berechnung der Anzahl von Molen

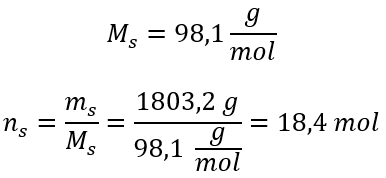
Schritt 4. Berechnung der Stoffmengenkonzentration wissend, dass sie die Anzahl der Mole der Substanz in 1 dm³ der Lösung ist

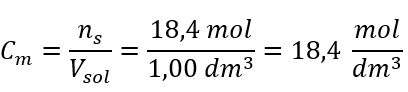
Methode 2 Verwendung des Verhältnisses zwischen prozentualer Konzentration und Stoffmengenkonzentration

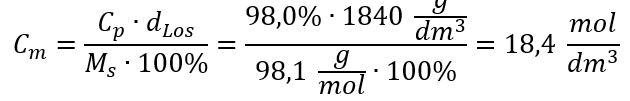
Antwort: Stoffmengenkonzentration dieser Säure beträgt 18,4 mol/dm³.