A homogeneous mixture of at least two substances is considered a solution. Although we think of a solution mainly as a liquid, gaseous and solid mixtures are also solutions. Nevertheless, a very large group of chemical reactions, both on a laboratory and industrial scale, occurs in an aqueous environment. There are three types of liquid solutions – the solvent is always liquid, but the solute can be a gas, liquid or solid. Among the examples are aqueous solutions of hydrogen chloride, ethanol and kitchen salt.

Describing the composition of the solution
The most important feature of any solution is the definition of its composition. The ability to determine the composition of a solution and to recalculate it depending on the units of interest is a basic skill of every chemist. The amount of a given ingredient in a mixture can be defined in various ways, e.g. by mass, volume or molarity.For this reason, there are also several types of concentrations, defining the dependence of the component’s amount on the amount of the solution or mixture. Most often, when describing the composition of solutions, we use the terms: mass fraction, volume fraction, mole fraction and molar concentration. Fractions indicate what part of a given mixture does the ingredient of interest account for. They can be expressed in units of mass, volume or moles of the compound.
Molar concentration
This is the most frequently chosen concentration, due to the convenience of use by determining the number of moles of the substance contained in the volume of the solution. The theoretical basis is the statement that solutions of two different substances of the same concentration and volume, at the same temperature, contain the same number of moles, and therefore the same number of molecules of the solute. On the basis of this relation, for solutions with equal molar concentrations it is possible to mix appropriate volumes of solutions to achieve the correct proportion of the number of moles determined by the stoichiometric coefficients. This means that, if thinking of A + B → C type reactions, where one mole of substance A reacts with one mole of substance B, equal volumes of both solutions with the same molar concentration must be mixed in order for the reaction to proceed completely. In the case of an A + 2B → C type reaction, i.e. one mole of substance A reacts with two moles of substance B, one volume of solution A should be mixed with two volumes of solution B. In this case, there is also another solution, because instead of using equimolar solutions in a 1:2 volume ratio, one may use one volume of solution A and one volume of solution B of twice the concentration. Molar concentration, denoted by Cm, defines the number of moles of a substances contained in a volume unit, most often in 1 dm3, of a solution.
The formula enabling the calculation of the molar concentration is the quotient of the number of moles of the substance (ns) and the total volume of the solution (Vsol) in dm3:
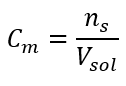
Using the basic volume unit according to the SI system, i.e. cubic meter, kilomoles should be used as the unit of the amount of the substance. However, this is not a major computational problem, because 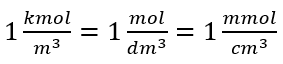 .
.
The unit of molar concentration Cm is defined as mole per cubic decimeter, often noted as M.
1 mol/dm3 = 1M

The use of molar concentration
a) Calculation of the molar concentration based on the content of the component in the solution
Example 1. The solution contains 30 g of potassium hydroxide in 3.0 dm3 of the solution. Calculate its molar concentration.
Step 1. Calculation of the molar mass of KOH
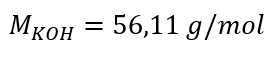
Step 2. Calculation of the number of moles of KOH in the solution
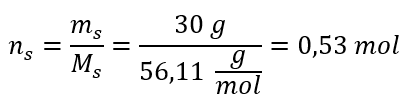
Step 3. Calculation of the molar concentration using the formula
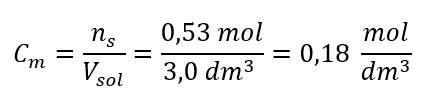
Answer: The molar concentration of a potassium hydroxide solution containing 30 g of the substance in 3.0 dm3 of the solution is Cm =
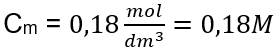
b) Preparation of a solution with a given concentration
Example 2. Calculate the mass of glucose (C6H12O6) required for the preparation of 300 cm3 of a solution with a concentration of 0.32 mol/dm3.
Step 1. Calculation of the molar mass of glucose
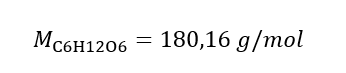
Step 2. Calculation of the mass of glucose needed, using the converted molar formula, knowing that 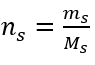 :
:
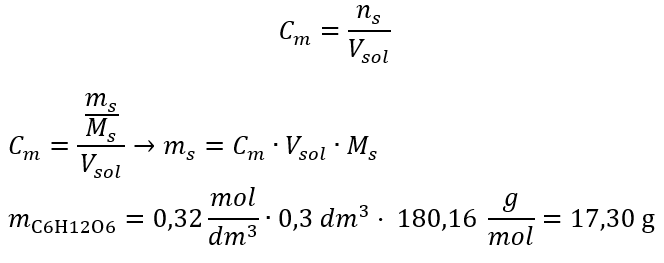
After these calculations, we know that in order to prepare such a solution, 17.30 g of glucose should be weighed and transferred quantitatively to a 300 cm3 volumetric flask.
Answer: To prepare 300 cm3 of a glucose solution with a molar concentration of 0.32 mol/dm3, 17.30 g of the substance should be weighed.
c) Dilution and concentration of concentrated solutions
Using the molar concentration, we can also prepare a solution of a given concentration (Cm2) by diluting the concentrated solution (Cm1), where:
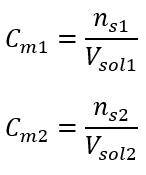
During dilution, only the volume of the solution changes, the number of moles of the solute remains unchanged. So one may assume that:
![]()
By transforming the formula for molar concentration, we obtain the following relations:
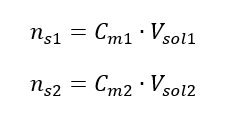
Knowing that we get the equation:
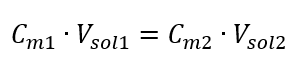
The formula for the dilution of solutions, with the consideration of molar concentration, including the newly obtained (Cmx) can be noted as:
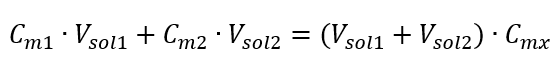
Example 3. What volume of 0.150 mol/dm3 acid can be obtained by diluting 250 cm3 of a 0.750 mol/dm3 solution of this acid with water?
Step 1. Transformation of the formula with the assumption that the water concentration is Cm2 = 0 mol/dm3.
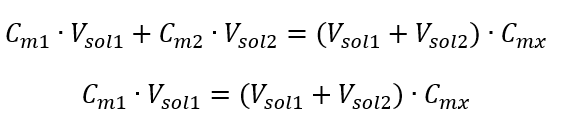
Step 2. Total volume calculation (Vx)
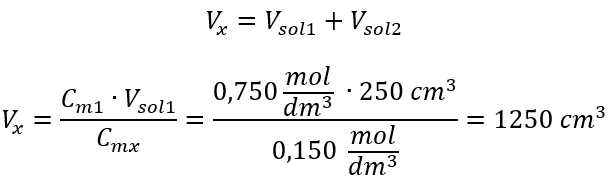
Alternatively, the relations of permanence of the number of moles during dilution can be used:
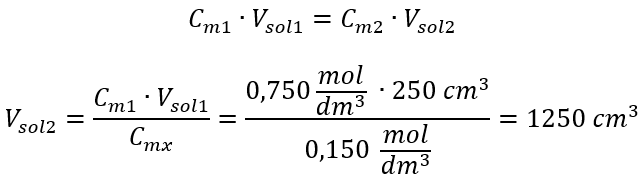
Answer: To dilute the acid to the required concentration, 1.25 dm3 of water must be used.
Example 4. Calculate how much water must be evaporated from 300 cm3 of a solution with a concentration of 0.125 mol/dm3 to obtain a solution with a concentration of 1.50 mol/dm3.
Step 1. Transformation of the formula for the change in molar concentration with the assumption that the molar concentration of water is Cm2 = 0 mol/dm3.
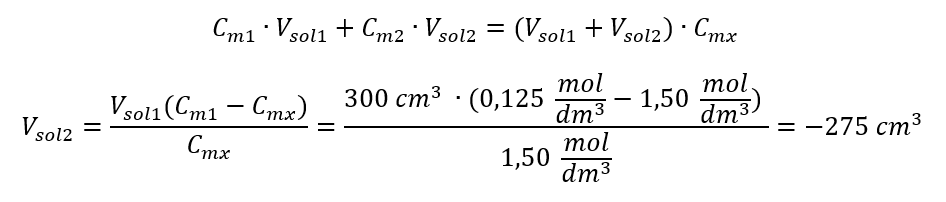
Answer: To concentrate the solution, 275 must be evaporated.
The conversion of molar concentration vs. percentage concentration
In everyday laboratory work, it is necessary to convert different concentrations of solutions. Most often, molar concentration and percentage concentration are used. It is possible to switch between them using the density of the solution. This parameter must be introduced to the formulas for the concentrations of interest:
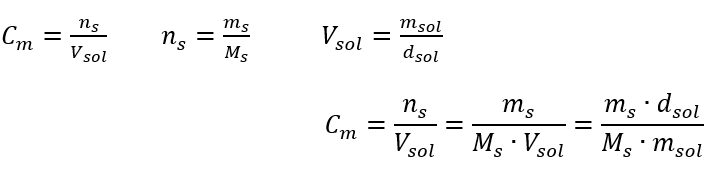
In the transformation, we can see the ratio of the substance mass to the mass of the solution, which is the basis of the percentage concentration, expressed by the formula:
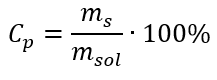
Substituting the formula for the percentage concentration into the previously transformed formula for the molar concentration, we get a relation that allows us to freely switch between the two values:
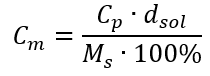
The only limitation of the formula is the use of appropriate units, so it is worth to consider them in all calculations.
Example 5. Calculate the molar concentration of sulphuric (VI) acid knowing that its percentage concentration is Cp = 98.0% and its density is d = 1.84 kg/dm3.
This can be calculated using two methods:
Method 1. In a few steps, without using a formula
Step 1. Calculation of the mass of 1.00 dm3 of the acid
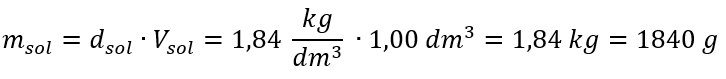
Step 2. Calculation of the mass of the acid taking into account the percentage concentration
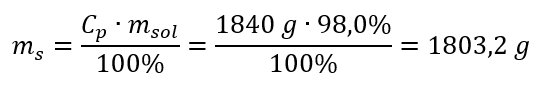
Step 3. Calculation of the number of moles
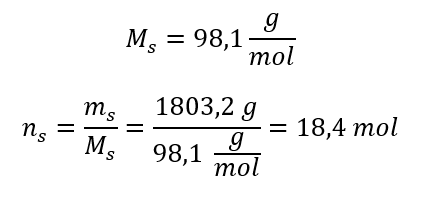
Step 4. Calculation of the molar concentration knowing that it is the number of moles of the substance in 1 dm3 of the solution
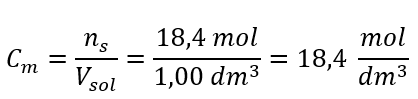
Method 2. Using the relation between percentage concentration and molar concentration
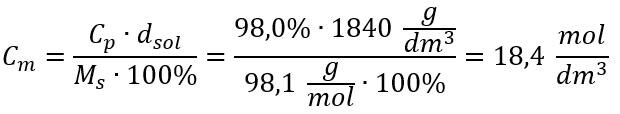
Answer: The molar concentration of this acid is 18.4 mol/dm3.