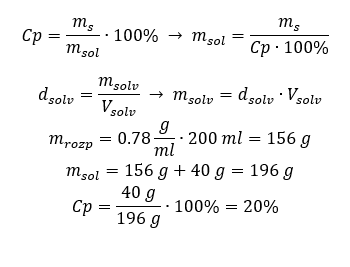In chemistry, we often use terms such as “concentrated solution”, “diluted solution” or “saturated solution”, but they give us only a basic outline of whether the solution contains a large or a small amount of a particular substance. However, there are a few methods which help us accurately determine the quantitative composition of a given solution. One of them is discussed in the following article.

Definition of percentage concentration
The term “concentration” refers to a measure of the amount of a given substance contained in a particular solution. Concentration can be expressed in units based on the measures that we use, for example in moles, grams or in percentage. Percentage concentration indicates how many parts by mass of the solute are included in 100 parts by mass of the solution. In other words, it is the number of grams of the solute in 100 g of the solution. For example, if we buy milk labelled 3.2%, it means that 100 g of the milk contains 3.2 g of fat. Percentage concentration is abbreviated as Cp.
General formula of percentage concentration
To derive the formula for percentage concentration, one must remember that the mass of a solution (msol) contains not only the mass of the solvent (msolv) but also the mass of the solute (ms):
msol = msolv + ms
For instance, if we take a 4% solution with a mass of 100 g, we know that Cp = 4%, so the mass of the substance is 4 g. The definition of percentage concentration indicates that if the mass of the solution is 100 g, then the mass of the solvent is 96 g.
Percentage concentration can be calculated with the following formula:
Cp = (ms/msol) · 100%
As we can see from the formula, if we know the mass of the solution and the mass of the substance, we can easily calculate the percentage concentration. For example, if we know that the solution weighs 450 g and the solute weighs 15 g, then by inserting these numbers to the formula, we obtain the following:
Cp = (15/450) · 100% = 3.3%
Calculating the mass of individual ingredients in a solution
Each formula, including that for percentage concentration, can be rearranged. If we know the mass and percentage concentration of the solution, we can calculate the mass of the solute. Similarly, if we know the percentage concentration and the mass of the substance, we can calculate the mass of the solution. In addition to rearranging the formula, we can also use appropriate proportions.
Example 1. How many grams of sugar do we need to prepare 300 g of a 10% solution?
We know from the instructions that the solution’s mass is 300 g and that its percentage concentration is 10%. The mass of the solute can be determined with two methods.
Method 1. Rearranging the formula
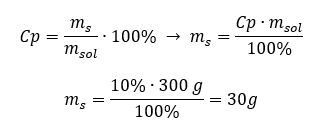
Method 2. Using the proportions, knowing that the 10% solution contains 10 g of sugar in 100 g of the solution: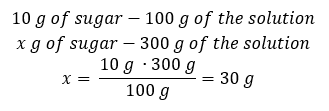
Both methods will lead us to the conclusion that the preparation of 300 g of a 10% solution will require 30 g of sugar.

Example 2. In how many grams of water do we have to dissolve 10 g of a substance to obtain a 50% solution?
We know from the instructions that the mass of the substance is 10 g and that the percentage concentration of the solution is 50%. This implies that 100 g of the solution contain 50 g of the substance. The mass of the solution can be determined with two methods. Please note that the mass of the solution is not equal to the mass of the solvent. To calculate the mass of the solvent, we have to subtract the mass of the substance from the mass of the solution.
Method 1. Rearranging the formula
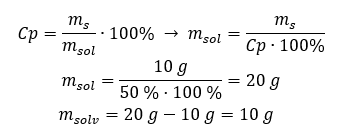
Method 2. Using the proportions, knowing that 100 g of the solution contain 50 g of the substance.
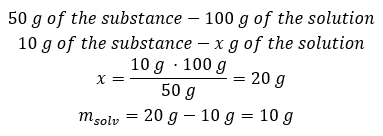
Regardless of the method we use, the answer will be that in order to obtain a 50% solution, we must dissolve 10 g of the substance in 10 g of water.
Preparing solutions
A key element of work in a laboratory is the knowledge of how to prepare solutions with particular concentrations. For that purpose, we have to know the mass of its ingredients. A previously calculated mass of a substance should be dissolved in an accurately measured volume of a solvent. The required volume can be calculated if we know the mass and density of the liquid. Solution density is a physical value specific to each liquid, which defines the solution’s mass per unit of volume. That value is closely related to temperature. If we know that the solution density is 2.03 g/ml, then we also know that 1 ml of the solution weighs 2.03 g. We usually use the following units of density: g/ml = g/cm3, g/l = g/dm3, but we there are also others, such as kg/m3. Solution density is calculated with the following formula: dsol=msol/vsol, where msol is the solution’s mass, and Vsol is its density. If we know the volume and density of the solution, we can calculate its mass.
Example 3. What is the mass of 20 ml of a solution with a density of 1.201 g/ml?
Method 1. Rearranging the formula
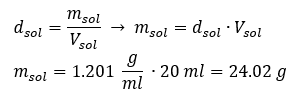
Method 2. Using the proportions, knowing that 1.201 g of the solution has a volume of 1 ml
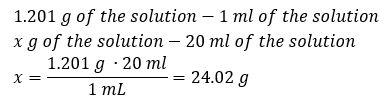
Both methods have demonstrated that the solution with a density of 1.201 g/ml and a volume of 20 ml has a mass of 24.02 g.
If we know the density, we can perform even more calculations in the context of percentage concentration.
Example 4. How many grams of salt are contained in 10 ml of a 15% solution if its density is 1.035 g/ml?
Method 1. Rearranging the formulae
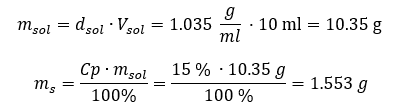
Method 2. Using the proportions
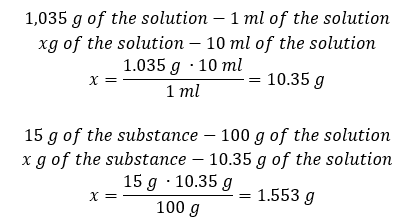
Both methods have demonstrated that to prepare 10 ml of a solution with Cp = 15% and a density of 1.035 g/ml, we have to weigh out 1.553 g of salt.
Example 5. What is the percentage concentration of a solution produced by dissolving 40 g of a substance in 200 ml of ethanol with a density of 0.78 g/ml?
To make the calculation, we can use the formula for percentage concentration. The solution mass can be calculated by adding up the masses of the solute and of the solvent. The mass of the solvent is unknown, but we do know its density and volume, so the missing data can be calculated by rearranging the formula for density.