Stoichiometry is the branch of general chemistry that deals with calculations concerning the quantitative course of chemical reactions. When working in the laboratory, it is very often necessary to know how much (mass, volume, molecules) of the substrates we need to use in order for the chemical reaction we are carrying out to take place completely or to obtain the amount of product we want. Sometimes it is also necessary to calculate excess or lacking substrate that caused the experiment to run differently than expected. Each of these calculations follows directly from the quantitative interpretation of the chemical reaction equation and uses the laws of conservation of mass. These types of equations are called stoichiometric calculations.

What do we need to know?
In order to use stoichiometry, we need to have knowledge in a number of areas, including: chemical reaction equations, stoichiometric coefficients, mole and molar masses and molar volumes of gases and Avogadro’s law. Using knowledge of the stoichiometry of chemical reactions, many calculation problems can be solved, such as:
- elemental analysis,
- molar calculations,
- mass calculations,
- calculation of non-stoichiometric mixtures with the possibility of determining the limiting substance in the reaction,
- reaction yield.
Molar mass
Due to the inconceivably small mass of individual atoms and molecules, the unit (u), expressing atomic mass, was created. In practice, this is a value equal to 1/12 of the mass of the carbon isotope 12C. This portion of a substance is closely related to Avogadro’s constant and is determined as the number of grams of a substance that contains 6.022·1023 atoms, molecules or ions. The molar mass [M] is numerically equal to the atomic or molecular mass, and the unit is g/mol.
Molar volume of substance [Vm]
This is a substance-specific value that strongly depends on temperature and pressure conditions. This is the volume of the substance occupied by one mole of it. Under normal conditions, a constant value of 22.4 dm3 is adopted.
Law of constant composition and conservation of mass
Every chemical compound, irrespective of its origin and method of obtaining it, has a well-defined and constant qualitative and quantitative composition. Sulphur (IV) oxide, for example, always contains 50 wt% sulphur and sulphur (VI) oxide 40 wt% of this element. In a closed system, the mass of the resulting products is equal to the mass of the substrates consumed during the reaction. The law of conservation of mass is reflected in the need to balance each chemical reaction equation with the appropriate chemical coefficients so that the two sides of the equation are equal in terms of the number of atoms present. Stoichiometric ratios reflect the molar ratios of the reactants present in the chemical reaction.
Chemical reaction equation
All the information needed on the relative relationships between chemical substances is derived from their chemical reaction equation. It provides some important relative and quantitative information.
Example 1.
From the equation for the synthesis of ammonia, which follows the reaction:
![]()
we can perform several interpretations – molecular, molar, molar masses, molar volumes and molecular numbers.
a) Molecularly, we can read that three molecules of hydrogen react with one molecule of nitrogen to form two molecules of ammonia.
b) This also means that three moles of hydrogen react with one mole of nitrogen to form the product of two moles of ammonia.
c) Using the periodic table of chemical elements, which contains the molar masses of the individual atoms, we can also conclude from the equation that 6 g of hydrogen has completely reacted with 28 g of nitrogen to form 34 g of ammonia.
d) Then, assuming normal conditions, we know that one mole of gas occupies 22.4 dm3. This allows us to conclude that 67.2 dm3 of hydrogen reacts with 22.4 dm3 of nitrogen to form 44.8 dm3 of ammonia.
e) Another useful relationship is Avogadro’s law, which states that equal volumes of different gases contain the same number of particles under the same conditions of pressure and temperature. Knowing Avogadro’s constant of 6.022·1023, we know that we need 3·6.022·1023 hydrogen molecules and 6.022·1023 nitrogen molecules to carry out the complete chemical reaction for the synthesis of ammonia. The reaction yields 2·6.022·1023 ammonia molecules.
Example 2.
The combustion reaction of magnesium in chlorine occurring according to the equation:
![]()
allows us to come up with interpretations similar to the previous example.
a) Even at first glance, the equation presented allows us to conclude that, in order to obtain one molecule of magnesium chloride, we must supply one molecule of magnesium and one molecule of chlorine as substrates.
b) This is of course equivalent to the number of moles present in the system, i.e. one mole of magnesium, one mole of chlorine, one mole of magnesium chloride.
c) For mass calculations, we know that 24 g of magnesium reacts with 71 g of chlorine to form 95 g of magnesium chloride.
d) Since only one gas, chlorine, is involved in the chemical reaction under consideration, we can also write for it that it occupies a volume of 22.4 dm3.
e) In particle counts, each component is equal to the other and takes the value 6.022·1023.
Percentage yield of chemical reaction [%W]
Stoichiometric calculations are also used to find out the yield of a reaction, i.e. the ratio of the actual amount of product obtained to the amount derived from the chemical reaction equation.
Example 1.
The oxidation reaction of 30 kg of sulphur(IV) oxide was carried out and, in the presence of a platinum catalyst, the product obtained was 34 kg of sulphur(VI) oxide. With was the yield of this process?
Chemical reaction equation:
![]()
From the recorded reaction, we can see that two moles of sulphur(IV) oxide produce the same amount of moles of sulphur(VI) oxide. Knowing the molar masses of the reactants, we know that stoichiometrically, assuming 100% yield, 128 g SO2 produces 160g SO3. With this knowledge, we can arrange the ratio:
0.128 kg SO2 – 0.160 kg SO3
30 kg SO2 – x kg SO3
From here we will find out the amount of sulphur(VI) oxide that would be produced at 100 per cent yield.
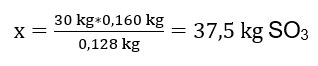
Knowing the theoretical and actual amount of SO3, we can calculate the yield at which the reaction occurred.
37.5 kg SO3 – 100% yield
34 kg SO3 – x% yield
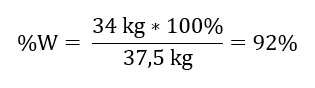
The oxidation of sulphur(IV) oxide to sulphur(VI) oxide using a platinum catalyst occurred with 92% yield.
Molecular and elemental formulas
Another application of stoichiometric calculations is to determine the formulae of simple chemical compounds. The molecular formula of a chemical compound is identical to, or an integer multiple of, the empirical formula. If we know that the general formula of a chemical compound is NxOy, the values of the stoichiometric indices can be calculated by dividing the mass per atoms by their atomic masses. If the molecular weight of a chemical compound is not known, but only its percentage composition, only the elemental formula can be given. It can be a true representation of the molecular formula or merely determine the ratio of the individual elements.
Example 1.
The molecular weight of the chemical compound is 92 u and it consists of 30.43% nitrogen and 69.57% oxygen. What is the molecular formula of the chemical compound?
Since the sum of the molecules present in the compound is 100% we can assume that:
92 u – 100%
This allows us to calculate the individual elemental contents:
92 u – 100%
x u of nitrogen – 30.43%
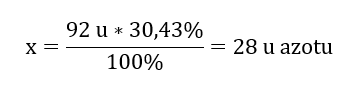
Hence we know that the mass per oxygen atoms is:
92 u – 28 u = 64 u
Knowing the individual masses of the elements, we can determine the stoichiometric indices:
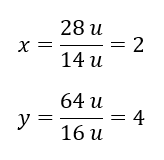
The molecular formula of this chemical compound is N2O4.
Example 2.
There are two elements in the chemical compound – oxygen at 60% and 40% sulphur. What is its elemental formula?
The general formula is SxOy, where x is 40% and y is 60%. Knowing the molar masses of the individual elements, this can be represented as follows:
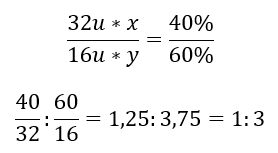
This means that in the given chemical compound, there are three oxygen atoms for every one sulphur atom. The elemental formula is SO3.

Excess and limiting substrate
In the case of reactions in which the reactants are present in ratios divergent from their corresponding stoichiometry, one of the reactants will react completely and the reaction will stop. It is then present in the form of the limiting reactant, while the second reactant will be in the system in excess and will also still be present in the system in its primary form when the reaction is complete.
Example 1.
In the laboratory, 40 cm3 of a 0.25 M aluminium sulphate solution was reacted with 50 cm3 of a 0.5 M barium chloride solution. How many grams of precipitate will be formed?
Chemical reaction equation:
![]()
The first step to knowing the actual course of a reaction is to determine the actual number of moles of the substances involved in the reaction.
nAl2(SO4)2: C Al2(SO4)2 · V Al2(SO4)2 = 0.25 · 0.04 dm3 = 0.010 mol
nBaCl2: C BaCl2 · V BaCl2 = 0.5 · 0.05 dm3 = 0.025 mol
The second step is to determine the deficit substrate based on the stoichiometry of the reaction – this will determine the amount of precipitate formed.
1mol Al2(SO4)3 – 3mol BaCl2
0.010 mol Al2(SO4)3 – x mol BaCl2
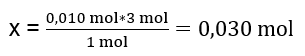
In order to carry out the reaction completely, having 0.010mol Al2(SO4)3, it is necessary to add 0.030mol BaCl2 to the system. However, only 0.025mol of barium chloride reacts, which means it is in deficit and will limit the reaction. Therefore, the amount of precipitate formed in the reaction should be calculated from the amount of this substrate.
The number of moles of barium chloride used according to the stoichiometry of the reaction is equal to the number of moles of the precipitate formed, thus:
nBaSO4 = nBaCl2
0.025mol BaSO4 = 0.025mol BaCl2
Knowing the number of moles of barium sulphate, we can calculate its mass:
mBaSO4 = nBaSO4 · MBaSO4
mBaSO4 = 0.025mol · 233.393 g/mol = 5.835g
The reactions and amounts of substrates given in the task produce 5.835g of barium sulphate precipitate.