The energy of chemical reactions is one of the important elements that allow us to understand the transformations that occur in a chemical reaction. During such a transformation, chemical compounds are produced with a structure and chemical composition different than those of the raw materials they are made of. In the course of a chemical reaction, the bonds existing between the atoms of the molecules used as reactants are broken off and new bonds are produced – present in the products.

The system and environment of a chemical reaction
For the proper interpretation of a chemical reaction in terms of energy, we need to have some knowledge about the following:
- System: a separated area of matter with clear boundaries. The type of the system is important: it is open if the reaction involves the exchange of energy and matter, closed if the reaction only involves the exchange of energy, or isolated if neither energy or matter is exchanged.
- Environment: anything that is not included in the system but is located nearby.
- System components: all substances which are located in the analysed system and have their characteristic chemical properties.
The energy of chemical bonds
The energy effect that characterises any chemical reaction is the result of changes occurring while breaking off and producing new bonds between atoms. The fact is that each break of a chemical bond is intrinsically linked with the absorption of an appropriate amount of energy, while the formation of a new bond causes the production of energy. The release of energy to the environment can have different effects: heat, light, work or electricity. Each of these processes is a component factor that affects the general change in the internal energy of the system in which the reaction takes place. It is important that, regardless of whether the reagents must draw or give up energy during the transformation, a certain amount of energy is always required to initiate the whole process.
The first law of thermodynamics
The first important rule concerning the energy of chemical reactions is the relationship formulated in the first law of thermodynamics, stating that the internal energy of a system which only exchanges energy with the environment (a closed system) can only be transformed into heat or work. This is reflected in the Helmholtz equation:
∆U = Q + W
Where ΔU denotes the change in internal energy, Q denotes heat, and W denotes work. We can notice from the formula that the internal energy of an isolated system, i.e., one that does not exchange energy or mass with the environment, is constant.
Components of the internal energy are all kinetic energies of atoms, ions, molecules, electrons, and components of atomic nucleus, which are currently in the reaction system, as well as the energies of their interactions, that is the energies of chemical bonds, interactions between charges, and so forth. Please note that the internal energy does not contain kinetic or potential energy of the system as a whole. The sum of kinetic and potential energies of the system as a whole and the internal energy is the system’s total energy (E).
System enthalpy (H)
This is another important concept related to the energy of chemical reactions, which in practice means the sum of the system’s internal energy and the product of its pressure and volume. In qualitative terms, it is the energy required to produce a system in vacuum (U), increased by work, i.e. the quotient of pressure and volume (pV), which the system must perform against external forces in order to achieve a volume different from zero. The relationship defining a system’s enthalpy is expressed as follows:
H = U + pV
A reaction occurring in such a system causes an infinitely small change in enthalpy:
dH = dU + dpV + pdV
If the reaction conditions are isobaric, so if the pressure during the process does not change, the second part can be omitted, because dpV=0. After substituting differentials for definite increments and after replacing the expression referring to the change of the system’s internal energy, we obtain the following relationship:
∆H = Q + W + p∆V
Assuming that the analysed process performs a volumetric work at a constant pressure, then W = -pΔV, and consequently:
∆H = Q – p∆V + p∆V
It follows from the equation that if the reaction occurs at a constant pressure, then the change in the system’s enthalpy is equal to the heat:
∆H = Q
Energetic capabilities of a reaction
Based on the formula derived above, which indicates that the change in the system’s enthalpy may be equal to the heat of the reaction, processes are classified according to thermal transformations. In terms of the direction of energy flow, we divide chemical reactions into:
- Exothermic reactions, which are such reactions where we can observe the emission of energy, for example in the form of heat, to the system’s environment. This happens when the sum of enthalpies of the products is lower than the sum of enthalpies of the substrates, so when ΔH<0.
- Endothermic reactions, so such chemical reactions which cause the absorption of energy from the environment. A condition for such a reaction is to deliver an appropriate amount of that energy. This applies to all transformations for which the total enthalpy of the products is higher than the total enthalpy of the substrates, so ΔH>0.
Notations of chemical reactions
Considering chemical reactions along with their energy demand and distribution, their specific heat effects are included in the notation of a chemical equation. For exothermic reactions, the absolute value of the existing heat effect is noted on the product side. Conversely, when noting down an endothermic reaction, the absolute value of the absorbed energy is noted on the substrate side. To give an example:
- Exothermic reaction:
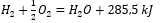
- Endothermic reaction: 2H3PO4 + 3Mg(OH)2 + 407kJ = Mg3(PO4)2 + 6H2O
Another way is to note down a chemical equation together with the energy effect value given aside. In this case, the value representing the energy of an exoenergic reaction is negative, while it is positive for an endoenergic reaction. For example:
- Exoenergic reaction: Fe + S → FeS ∆H= -95,2 kJ/mol
- Endoenergic reaction: FeS → Fe + S ∆H= 95,2 kJ/mol
Hess’s law
It constitutes a foundation for thermochemical computations, stating that the heat effect is always the same regardless of the way the reaction is carried out. This allows us to calculate the standard enthalpy of a reaction (ΔrHϴ), assuming the use of standard conditions, that is a pressure of 105 Pa and any temperature. Since enthalpy is a function of state, its variability depends on only two values: in the initial and final states, which in a chemical reaction represents the state of substrates and the state of products, respectively. The Hess’s law is expressed by an equation that contains stechiometric coefficients (v) and standard molar enthalpies of formation (ΔfHϴ):
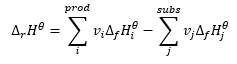
Standard molar enthalpy of formation
It is an enthalpy obtained by forming 1 mol of a particular chemical compound from elements in their basic states. The basic state is the most durable variant of the element in specific conditions. To give an example, graphite is the most durable variant of carbon at 25oC and 105 Pa. Conversely, at a high temperature and pressure, a stable form of carbon is diamond.
For each reactant that participates in a reaction in its basic condition, the value of standard molar enthalpy of formation is zero. Usually these are individual atoms of noble gases or the most durable variants of other gases in specific conditions. For a standard pressure (105 Pa) and temperature (normally 25oC), the values of standard molar enthalpies of formation of compounds are gathered in chemical tables. The unit of that value is . The Hess’s law applied to chemical reactions implies that the reaction’s enthalpy value is independent of the number of intermediate reactions. The only key information is that particular substrates are used to obtain particular products.
The synthesis of carbon dioxide
The synthesis of carbon dioxide can be carried out in various ways, but according to the Hess’s law each of them leads to the same value of changes in standard enthalpies.
- Direct synthesis
- The ynthesis of carbon (II) oxide + oxidation of the compound to carbon (IV) oxide
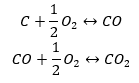
When we read out the values of standard enthalpies of formation of the compounds from the table and substitute them in the chemical equations, we will see that the enthalpy for each method is the same: -393.5 kJ/mol.
Kirchhoff’s law
It enables us to transform the computations in order to calculate the standard enthalpy of a reaction for a certain temperature, if we know its value at a different temperature. We also know the relationships between the molar heat of all reactants and the temperature. The law can be applied, as the change in the enthalpy of the reaction depends on the conditions in which it was determined: it varies along with changing temperature and pressure. The derivation of the formula should be started by defining the thermal capacity, that is the ratio of supplied heat to the rise in temperature:
![]()
Assuming isothermal conditions, we can make the following transformation:
![]()
Integration of the resulting equation and the conversion of thermal capacity into the part representing the change in standard thermal capacity is reflected by the equation provided by the Kirchhoff’s law:
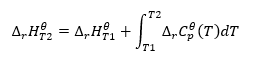
For standard conditions, the change in a reaction’s thermal capacity is defined by the equation with v-variables, being stechiometric factors, and , which represents the standard molar heat of a given reactant. When the temperature difference is small (up to 100K), the value of the standard molar heat of the reactant is assumed to be constant within a certain range. Then we can use the simplified form of the Kirchhoff’s law, assuming that the reactants’ thermal capacities do not depend on the temperature but on constant pressure, :
![]()