Electronegativity is a quantity that reflects the tendency of a given atom within a molecule to attract electrons towards itself. In practice, it is the ability of an atom or functional groups to attract electron density. The most commonly used scale associated with this quantity is the one introduced by Linus Pauling, which makes it possible to easily calculate the approximate nature of the bond.
Electronegativity characteristics
Homonuclear molecules, for example H2 and O2, have equal coefficients cA and cB in their molecular orbitals, which can be recorded as wave functions:
Ψ+AB = cAΨA + cBΨB
Ψ−AB = cAΨA − cBΨB
In this case, the orbital is characterised by its shape being symmetrical with respect to the centre of the molecule, and its electrical charge is equally symmetrically distributed within it. However, another example is heteronuclear molecules, in which it is virtually impossible to maintain equal coefficients, as well as full symmetry with respect to the centre of the molecule. When the energy level of atomic orbital ΨB is lower than the energy level of atomic orbital ΨA, the relation occurs, and the maximum of the electron probability density is shifted towards atom B. In practice, this results in a shift of the electron pair in the chemical bond, i.e. polarisation towards atom B. For example, in the lithium hydride molecule LiH this shift is towards the hydrogen atom, while in the hydrogen fluoride molecule HF it is towards the fluorine atom. This means that the hydrogen atom has a lower energy level than lithium, but a higher energy level than fluorine (read about halogens). Under these conditions, one of the atoms of both molecules takes on a negative charge denoted as -δ and the other is positive +δ. The general formula of such a molecule is A+δB-δ.
Charges of atoms
The aforementioned charge δ can take on different values depending on the elements bound by the chemical bond. Its value of 0 means that the charge of the electron pair is distributed symmetrically and the pair is located completely in the vicinity of the atom with a lower energy level, resulting in the transfer of both electrons to that atom. This creates an ionic bond between the elements. In the vast majority of chemical bonds, however, there are fractional charges, resulting in a state between covalent and ionic bond.
Dipole moment
A dipole is a molecule in which two poles – positive and negative – can be distinguished. The dipole moment, denoted by μ, is a measure of the magnitude of the electric charge shift in it. It is defined as the product of the absolute value of the electric charge (δ) contained in one of the poles and the distance from these poles (l):
μ = δ · l
A positive charge (δ+) and a negative charge (δ-) is called a partial charge and its location is attributed to a particular atom, but in reality it is only the greater or lesser probability of an electron being present around their nuclei. Such a phenomenon is sometimes confused with the processes of oxidation and reduction, but unlike the changes that take place in them, such charges being taken on by the atoms does not cause them to move to another oxidation state, so there is no electron exchange between them. The SI unit for expressing the dipole moment is the coulomb meter (C·m). However, in calculations the unit written in the CGS system, the debye (D), is most commonly used. One debye corresponds to a value of 3.33564·10-30 C·m. The largest theoretically possible dipole moment characterises molecules with a purely ionic bond. Whereas, the smallest occurs in molecules whose bond is purely covalent – the dipole moment is zero in this case. However, most are intermediate cases with varying particle characters.
Halogen dipole moment
Several relationships between electronegativity and dipole moment can be easily observed on specific chemical compounds.
Table 1 Dipole moments of hydrogen halides
| Compound | Experimentally determined dipole moment [μ, D] | Bond length [pm] | Product of elemental charge and dipole length [e·l, D] | Share of ionic character [%] | Difference in the electronegativity of halogen and hydrogen |
| HF | 1.98 | 92 | 4.42 | 45 | 1.9 |
| HCl | 1.08 | 128 | 6.15 | 18 | 0.9 |
| HBr | 0.79 | 143 | 6.87 | 12 | 0.7 |
| HI | 0.38 | 162 | 7.78 | 5 | 0.4 |
The ratio μ/(e·l’), i.e. the actual dipole moment to the dipole moment that corresponds to an ionic bond, can provide a measure of deviations from the fully covalent bond. The product of this relationship in the form of (μ/(e·l’))·100% represents the percentage of the ionic character in the bond. This is only an approximate value, as the dipole moment depends not only on the polarity of the bond, but also on the behaviour of the free electron pairs. It happens that the electron cloud can be shifted to the outside of the molecule, the consequence being that the equation for determining its dipole moment has an additional component. In the case of the ammonia molecule, the cloud is directed in line with the dipole moment of the bond, resulting in an increase in the resultant dipole moment. In contrast, the opposite is true for the carbon monoxide molecule, where the cloud is directed in the opposite direction and consequently reduces the resultant dipole moment.
Electronegativity
It is a dimensionless empirical quantity that reflects the tendency of a given atom within a molecule to attract electrons towards itself. In practice, it is the ability of an atom or functional groups to attract electron density. The most commonly used scale associated with this quantity is the one introduced by Linus Pauling, which makes it possible to easily calculate the approximate nature of the bond. The scientist used the following method to calculate the electronegativity of the individual elements:
We assume that DA-A and DB-B are the bond energies of the two-atom molecules (A2, B2). We designate the binding energy that occurs in the molecule as DA-B. Empirically, it has been shown that if such a bond contains little or no ionic character, the difference between the DA-B values and the geometric mean of the DA-A and DB-B energy values is equal to or close to zero. When the A-B bond has clear deviations from the covalent character, this difference takes on positive values, which increase as the proportion of the ionic character increases. The difference between the electronegativity (x) of the two atoms involved in the bond is expressed by the formula:
Hence, if Pauling assumed an electronegativity of fluorine of 4.0 in his calculations, it is possible to calculate the subsequent electronegativities of the elements. If we know the xA value of the atoms of element A and the value of the coefficient Δ’ then we can calculate the xB value using the above equation. The Pauling scale is constructed in such a way that its values agree approximately with the values of the dipole moment of the bond formed by the atoms under consideration, as we can see from the example in Table 1, which contains the values determined for hydrogen halides. In addition to the scale described above, there are several more described in the scientific literature, including the electronegativity described by:
- Mulliken, whose work assumed that the electronegativity of an element is directly proportional to the sum of its electron affinity and ionisation energy. Electron affinity, which is the amount of energy that is released due to the attachment of an electron to a neutral atom, and the ionisation energy equal to the amount of energy required to detach an electron from a neutral atom. The highest electronegativities are therefore characteristic for atoms that exhibit high electron affinity and high ionisation energy.
- Allred and Rochow, who assumed the proportionality of electronegativity to the measure of the force with which the atomic nucleus (Z) acts on the valence electrons, recorded as
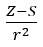(r – atomic radius, S – screening constant). According to their theory, electronegativity (x) of the elements can be calculated using the formula:
At each scale, the electronegativity of hydrogen is close to the value of 2.2, with other values varying slightly. Examples of the electronegativities of elemental atoms calculated according to the Pauling, Mulliken and Allred and Rochow scales are shown in Table 2 below.
Table 2 Electronegativities of example elements on the Pauling (P), Mulliken (M) and Allred and Rochow (AR) scales
| Atom | P | M | AR |
| F | 3.98 | 3.90 | 4.10 |
| O | 3.44 | 3.04 | 3.50 |
| N | 3.04 | 2.28 | 3.07 |
| Cl | 3.16 | 2.95 | 2.83 |
| C | 2.55 | 1.75 | 2.50 |
| H | 2.20 | 2.21 | 2.20 |
| Si | 1.90 | 2.25 | 1.74 |
| F | 0.82 | 0.77 | 0.91 |
| Rb | 0.82 | 0.50 | 0.89 |
| Cs | 0.79 | – | 0.86 |
| Fr | 0.70 | – | 0.86 |
Despite the discrepancies in the calculations with the three methods, fluorine has the highest electronegativity at each scale, followed by oxygen, nitrogen and chlorine. The lowest values were determined for francium, caesium, rubidium and potassium. Elements that are typically non-metals have electronegativities above the value of 2, typical metals have electronegativities below 2. The standard value is the aforementioned electronegativity of hydrogen of approximately 2.2.
Electronegativity in the periodic table
Like many other properties, electronegativity is also reflected in the arrangement of the chemical elements on the periodic table. In the group, the electronegativity decreases with increasing number of shells and metallic character, so it increases in the direction from francium to hydrogen. Over time, the electronegativity increases with an increase in the valence electrons present and a decrease in the non-metallic character, so from metals to noble gases.
Electronegativity and bond type – summary
By knowing the individual values of the electronegativity of the elements that form the chemical bond, we can deduce its nature. If the difference is between 0.0 and 0.4, the bond is covalent. When the difference is between 0.4 and 1.7, the bond is polarised covalent. A difference above 1.7 in the electronegativity of the elements suggests ionic bonding.