Comment décrivons-nous les couleurs? Modèles de couleurs indépendants

En 1931, à la demande de la Commission internationale de l’éclairage, un modèle de couleur indépendant des appareils a été développé. Il a été créé sur la base des recherches menées sur un groupe d’une vingtaine de personnes capables de distinguer correctement les couleurs. Ce groupe a été montré, dans un champ de vision très étroit (2o), de différentes couleurs et avait la tâche de les différencier. Analyser la statistique des réponses à un permis de développer un modèle d’observation standard. Il montre les capacités humaines moyennes en termes de perception des couleurs (par exemple gamme de longueurs d’onde, sensibilité, etc.). Basé sur le modèle d’observation standard, le modèle CIE XYZ a été développé – le premier modèle de couleur indépendant de l’appareil. La méthode CIE XYZ est appelée un espace colorimétrique qui est pris comme référence et standard pour les autres espaces colorimétriques créés par la Commission internationale de l’électricité (CIE LUV, CIE Lab). Le concept des trois valeurs chromatiques de XYZ est basé sur l’idée de voir les couleurs, qui dit que l’œil est composé de trois types de photorécepteurs qui vous permettent de voir les trois couleurs de base (rouge, vert, bleu), tandis que toutes les couleurs sont des mélanges des trois couleurs de base. Par conséquent, la couleur est décrite dans les coordonnées trichromatiques X, Y, Z. Ces coordonnées correspondent aux pourcentages respectifs des trois couleurs de base R (rouge), G (vert) et B (bleu).

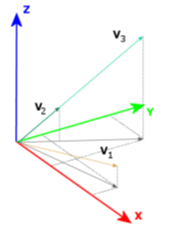
Fig. 1 http://home.agh.edu.pl/~tarasiuk/dydaktyka/doc/GFK/S/02%20Problem%20barwy%20i%20koloru.pdf

La description tridimensionnelle de CIE XYZ était supérieure en un espace CIE xyY bidimensionnel. Il convertit les composantes de couleur X, Y, Z en coordonnées trichromatiques x, y, Y. Les coordonnées x et y sont responsables de la chromaticité et Y de la luminosité. L’espace xyY est représenté dans l’espace colorimétrique, qui est le graphique de chromaticité, sous la forme d’un triangle de Maxwell ou d’un triangle chromatique. Ceci est présenté comme une zone délimitée par deux lignes – une courbe de couleur monochromatique et une ligne droite pourpre.

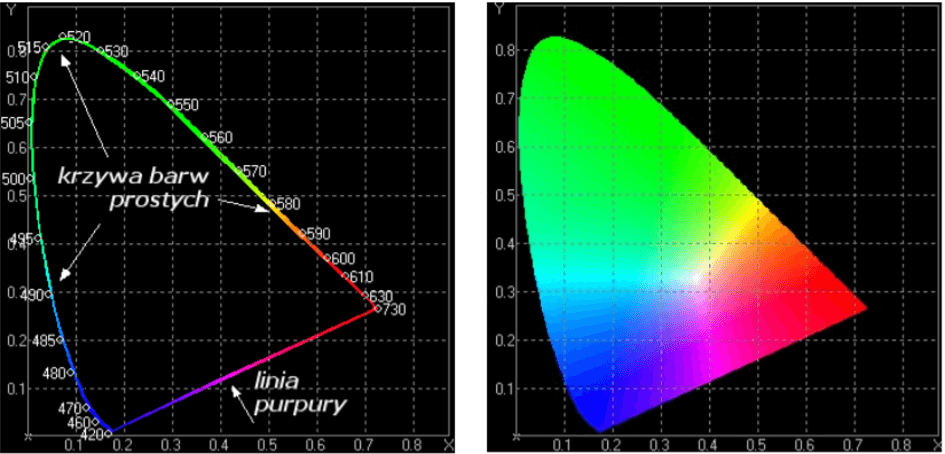
Fig. 2 http://home.agh.edu.pl/~tarasiuk/dydaktyka/doc/GFK/S/02%20Problem%20barwy%20i%20koloru.pdf

À la suite des travaux sur la question de perception de la différence de couleur, réalisée par Wright, MacAdam et Stiles, la question de l’uniformité de l’espace colorimétrique a été posée. Lorsque l’espace CIE XYZ détermine les plages de différence de perception des couleurs (Fig. Ci-dessous), des ellipses de différentes tailles (appelées ellipse de MacAdam) apparaissent. Ils seront formés dans les zones vertes, comme des ellipses de diamètre relativement grand et dans les zones bleues, mais ici de diamètre relativement petit. Ainsi, lorsque nous marquons deux points dans un tel espace, l’œil humain peut être perçu comme deux teintes subjectivement différentes. D’un autre côté, deux points également distants dans la gamme des couleurs vertes peuvent déterminer les couleurs entre l’œil humain ne remarquera pas la différence, c’est-à-dire qu’il s’agit d’une couleur déterminée subjectivement .

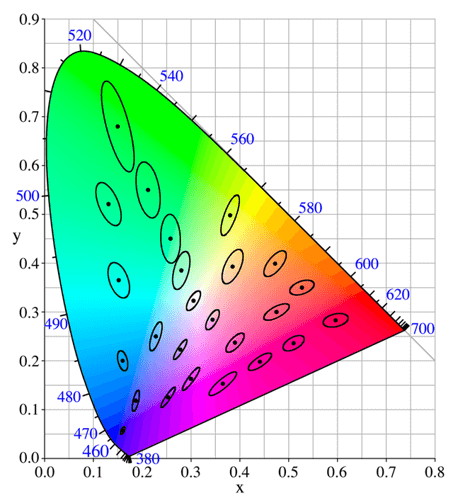
Fig. 3 https://stackoverflow.com/questions/25184748/represent-cie-1931-color-space

Grâce à des recherches sur l’uniformité de l’espace colorimétrique, CIE LUV et CIE Lab ont également été été elles. Le modèle CIE LUV a été créé (en 1960) à la suite de la transformation des variables xy en variables uv. Ils étaient censés mieux refléter les différences entre les couleurs. Au cours de recherches ultérieures, cependant, il s’est avéré qu’un tel ensemble de variables limite fortement les zones autour du brun, de l’orange et du jaune. Les teintes mentionnées sont très importantes dans la peinture, en particulier dans les photographies à l’huile ou dans la nature, c’est pourquoi de nouvelles tentatives de transformation ont dû être faites. En 1976, les variables u ‘et v’ ont été développées, ainsi que l’espace CIE LU’V ‘ . Il est important que la lettre “L” dans les noms provienne ici du mot “légèreté” et tout comme le “Y” dans le modèle xyY, elle définit la luminosité. Les deux représentations chromatiques obtenues sont illustrées dans la figure ci-dessous: a) Diagramme CIE uv b) Diagramme CIE u’v ‘[id de légende = “attachment_1250355” align = “alignnone” width = “945”] 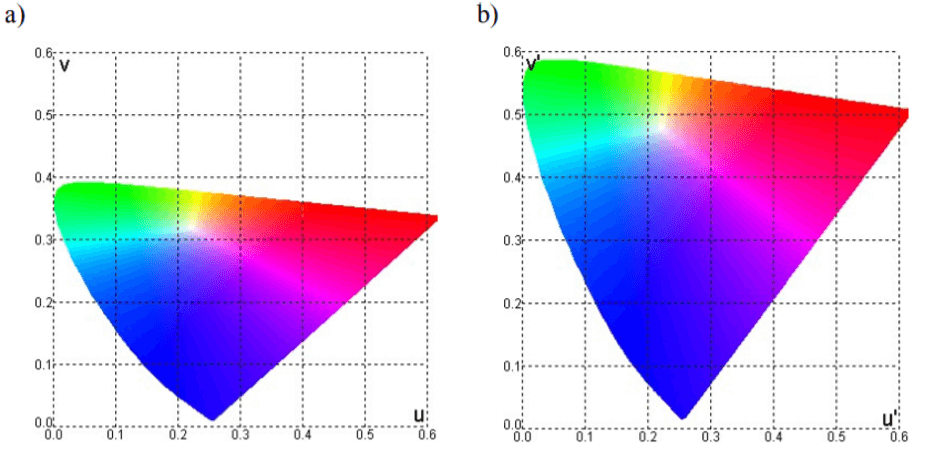Fig. 4 http://home.agh.edu.pl/~tarasiuk/dydaktyka/doc/GFK/S/02%20Problem%20barwy%20i%20koloru.pdf[/caption] Le deuxième modèle de couleur le plus utilisé utilisé de l’appareil est le CIE Lab . Il s’agit d’une autre transformation de l’espace CIE XYZ, créé en 1976. En définissant, sur une supposé que les couleurs qui sont à la même distance les unes des autres seront perçues comme également différentes. En supposant que la couleur ne peut pas être violette et bleu et jaune ou vert en même temps, les composants suivants ont été sélectionnés pour la description: L – luminosité (luminance), a – couleur du vert au magenta et b – couleur du bleu au jaune.

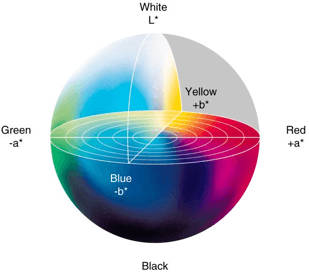
Fig. 5 https://www.researchgate.net/figure/CIE-LAB-1976-color-space_fig2_263697963

Cependant, un avantage important d’un modèle donné est la facilité de comparaison des couleurs. La différence entre les deux couleurs dans l’espace CIE Lab est exprimée en ΔE, qui est à partir de la relation suivante: 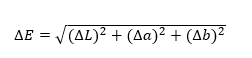ΔE est la distance euclidienne normale entre deux points dans l’espace tridimensionnel. On suppose qu’un observateur standard reconnaît la différence de couleur selon les indicateurs suivants: 0 <ΔE <1 – ne voit aucune différence, 1 <ΔE <2 – seul un observateur expérimenté remarque la différence, 2 <ΔE <3,5 – également un inexpérimenté l’observateur remarque la différence, 3,5 <ΔE <5 – l’observateur remarque une nette différence de couleur, 5 <ΔE – l’observateur perçoit les deux couleurs comme complètement différentes. Tout comme l’espace CIE XYZ, le modèle CIE Lab est lié à la perception directe des couleurs par l’œil humain. C’est pourquoi nous l’appelons un modèle de couleur indépendant de l’appareil. L’ espace colorimétrique CIE LCh utilise le même schéma que l’espace colorimétrique CIE Lab, mais utilise des coordonnées cylindriques au lieu de coordonnées rectangulaires. Dans cet espace colorimétrique, L est la luminosité et est le même paramètre que L dans l’espace CIE Lab, C est la saturation et h est la teinte. La valeur de saturation des couleurs C est 0 au centre de la sphère, qui est l’image de l’espace colorimétrique et augmente en fonction de la distance du centre. L’ombre est à l’angle dont la mesure commence sur l’axe + et est exprimée en degrés.

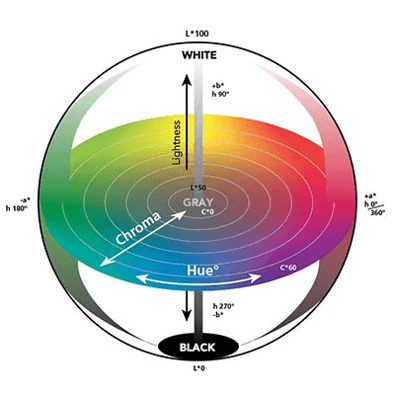
Fig. 6 https://www.xrite.com/blog/tolerancing-part-3

L’ espace colorimétrique Hunter Lab a été développé en 1966 par RS Hunter comme un espace coloreur plus homogène visuellement que le CIE 1931 Yxy et très similaire au CIE Lab. Il est actuellement utilisé dans divers domaines, y compris l’industrie de la peinture aux États-Unis, mais il est appliqué moins souvent que l’espace CIE Lab développé un peu plus tard, qui a gagné plus de supporters. Les échelles Hunter Lab et CIE Lab utilisent les fonctions légèrement différentes pour calculer les valeurs Lab en utilisant des composants trichromatiques XYZ comme arguments. Hunter Lab effectue la transformation en utilisant des racines carrées, tandis que le CIE Lab utilise les fonctions de racine cubique. Une autre différence est visible dans la gamme des zones de couleur individuelles. L’échelle Hunter se rétrécit dans la zone jaune de l’espace colorimétrique et se développe dans le bleu. L’échelle CIE Lab, en revanche, est légèrement élargie dans la zone jaune, ce qui est plus évident lorsque la valeur CIE de l’échantillon est inférieure à un. Un avantage supplémentaire de l’échelle CIE Lab est qu’elle aurait pu être mieux connue les différences de couleur pour les couleurs très sombres.

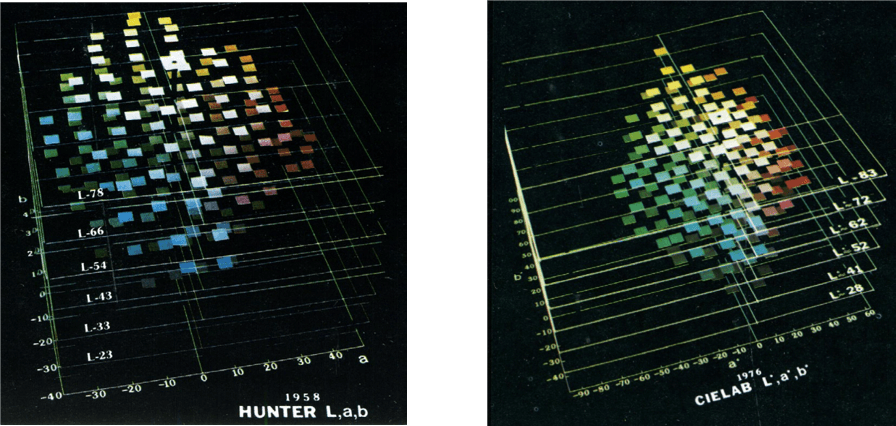
Fig. 7 http://pomiarbarwy.pl/?p=481