적어도 두 가지 물질의 균질 혼합물은 용액으로 간주됩니다. 우리는 용액을 주로 액체로 생각하지만 기체와 고체 혼합물도 용액입니다. 그럼에도 불구하고 실험실 및 산업 규모 모두에서 매우 큰 그룹의 화학 반응이 수성 환경에서 발생합니다. 액체 용액에는 세 가지 유형이 있습니다. 용매는 항상 액체이지만 용질은 기체, 액체 또는 고체일 수 있습니다. 그 예로는 염화수소, 에탄올 및 식염의 수용액이 있습니다.
솔루션 구성 설명
모든 솔루션의 가장 중요한 기능은 해당 구성의 정의입니다. 용액의 조성을 결정하고 관심 단위에 따라 다시 계산하는 능력은 모든 화학자의 기본 기술입니다. 혼합물에서 주어진 성분의 양은 질량, 부피 또는 몰농도와 같은 다양한 방법으로 정의될 수 있습니다. 이러한 이유로 용액 또는 혼합물의 양에 대한 성분의 양의 의존성을 정의하는 여러 유형의 농도도 있습니다. 대부분의 경우 용액의 구성을 설명할 때 질량 분율, 부피 분율, 몰 분율 및 몰 농도라는 용어를 사용합니다. 분수는 주어진 혼합물의 어떤 부분이 관심 성분을 설명하는지 나타냅니다. 화합물의 질량, 부피 또는 몰 단위로 표현할 수 있습니다.
몰 농도
이것은 용액 부피에 포함된 물질의 몰수를 결정하여 사용하기 편리하기 때문에 가장 자주 선택되는 농도입니다. 이론적 근거는 동일한 온도에서 동일한 농도와 부피를 가진 두 가지 다른 물질의 용액이 동일한 수의 몰수를 포함하므로 동일한 수의 용질 분자를 포함한다는 진술입니다. 이 관계를 기반으로 동일한 몰 농도를 가진 용액의 경우 적절한 부피의 용액을 혼합하여 화학양론적 계수에 의해 결정된 몰수의 정확한 비율을 달성할 수 있습니다. 즉, 물질 A 1몰과 물질 B 1몰이 반응하는 A+B→C형 반응을 생각하면, 같은 몰농도의 두 용액을 같은 부피로 섞어야 반응이 완전히 진행된다. A + 2B → C 유형 반응의 경우, 즉 물질 A 1몰과 물질 B 2몰이 반응하는 경우 A 용액 1부피와 B 용액 2부피를 혼합해야 합니다. 이 경우 등몰 용액 을 1:2 부피비로 사용하는 대신 A 용액 1부피와 농도의 두 배인 용액 B 1부피를 사용할 수 있기 때문에 다른 용액도 있습니다. C m 으로 표시되는 몰 농도는 용액의 부피 단위, 대부분 1 dm 3 에 포함된 물질의 몰수를 정의합니다. 몰 농도를 계산할 수 있는 공식은 물질의 몰수( ns )와 용액의 총 부피(V sol )의 몫(dm 3 )입니다.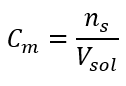 
SI 시스템에 따른 기본 부피 단위, 즉 입방 미터를 사용하여 물질의 양 단위로 킬로몰을 사용해야 합니다. 그러나 이것은 중요한 계산 문제가 아닙니다. 
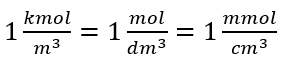. 몰 농도 Cm 의 단위는 입방 데시미터당 몰로 정의되며 종종 M으로 표시됩니다. 1 mol/dm 3 = 1M 
몰 농도의 사용
a) 용액의 성분 함량에 기초한 몰농도 계산 실시예 1. 용액은 용액 3.0dm3 에 수산화칼륨 30g을 포함한다. 몰 농도를 계산하십시오. 1단계. KOH의 몰 질량 계산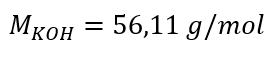 
2단계. 용액의 KOH 몰수 계산 
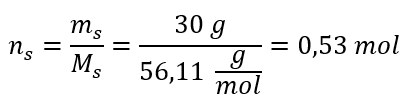3 단계. 공식을 사용하여 몰 농도 계산 
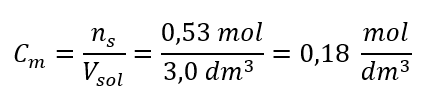답: 용액 3.0dm 3 에 물질 30g을 함유하는 수산화칼륨 용액의 몰 농도는 C m = 
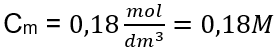b) 주어진 농도의 용액 준비 예 2. 0.32 mol/dm 3 농도의 용액 300 cm 3 를 준비하는 데 필요한 포도당(C 6 H 12 O 6 )의 질량을 계산하십시오. 1단계. 포도당의 몰 질량 계산 
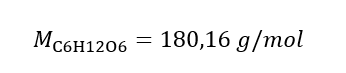2단계. 변환된 몰 공식을 사용하여 필요한 포도당의 질량 계산 
: 
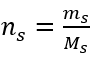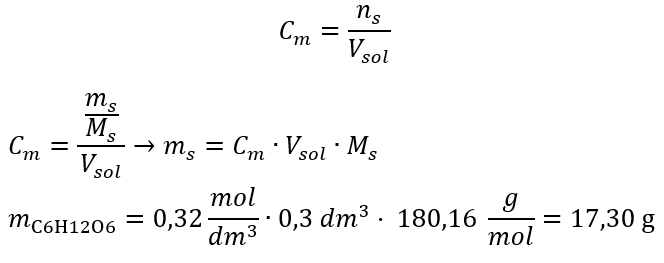이러한 계산 후, 우리는 그러한 용액을 준비하기 위해 17.30g의 포도당을 칭량하고 정량적으로 300cm 3 부피 플라스크로 옮겨야 한다는 것을 알고 있습니다. 답변: 몰 농도가 0.32 mol/dm 3 인 포도당 용액 300 cm 3 를 준비하려면 물질 17.30 g의 무게를 달아야 합니다. c) 농축 용액의 희석 및 농축 몰 농도를 사용하여 농축 용액(C m1 )을 희석하여 주어진 농도(C m2 )의 용액을 준비할 수도 있습니다. 
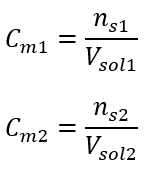희석하는 동안 용액의 부피만 변하고 용질의 몰수는 변하지 않습니다. 따라서 다음과 같이 가정할 수 있습니다. 
몰 농도 공식을 변환하여 다음 관계식을 얻습니다.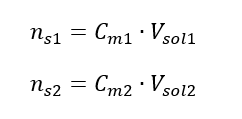 
우리가 방정식을 얻는다는 것을 알면: 
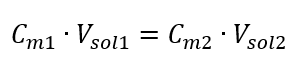새로 얻은 (C mx )를 포함하여 몰 농도를 고려한 용액 희석 공식은 다음과 같습니다. 
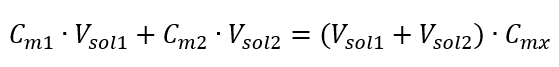예 3. 이 산의 0.750 mol/dm 3 용액 250 cm 3 를 물로 희석하여 얻을 수 있는 0.150 mol/dm 3 산의 부피는 얼마입니까? 단계 1. 물 농도가 C m2 = 0 mol/dm 3 이라는 가정 하에 공식 변환. 
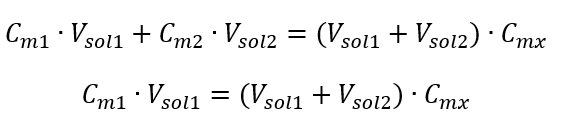2단계. 총 체적 계산(V x ) 
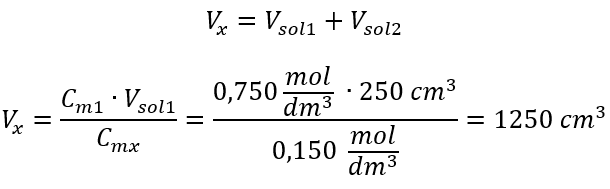또는 희석 중 몰 수의 영속 관계를 사용할 수 있습니다. 
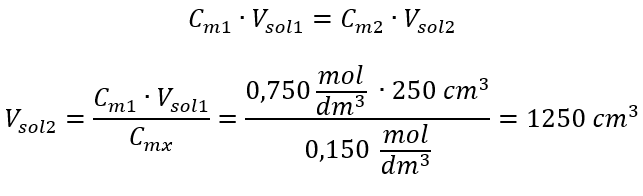대답: 필요한 농도로 산을 희석하려면 1.25dm 3 의 물을 사용해야 합니다. 예 4. 1.50 mol/dm 3 농도의 용액을 얻기 위해 0.125 mol/dm 3 농도 의 용액 300 cm 3에서 얼마나 많은 물을 증발시켜야 하는지 계산하십시오. 1단계. 물의 몰 농도가 C m2 = 0 mol/dm 3 이라는 가정 하에 몰 농도 변화 공식 변환. 
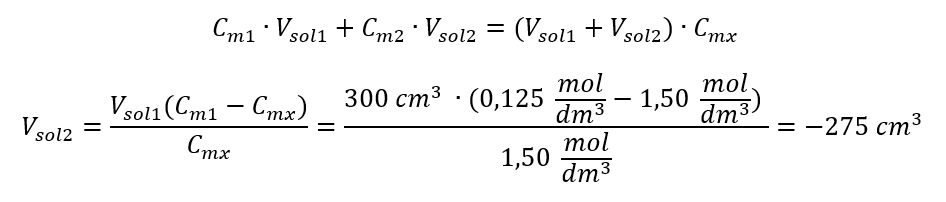답변: 용액을 농축하려면 275를 증발시켜야 합니다. 몰농도 대 백분율 농도의 변환 일상적인 실험실 작업에서는 다양한 농도의 용액을 변환해야 합니다. 대부분의 경우 몰 농도와 백분율 농도가 사용됩니다. 솔루션의 밀도를 사용하여 이들 사이를 전환할 수 있습니다. 이 매개변수는 관심 농도에 대한 공식에 도입되어야 합니다. 
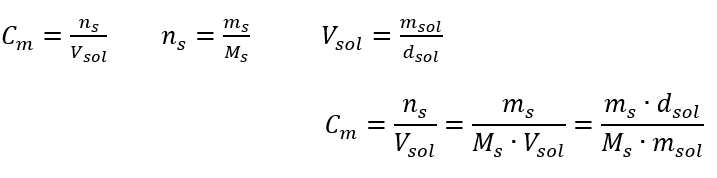변환에서 물질 질량 대 용액 질량의 비율을 볼 수 있습니다. 이는 다음 공식으로 표현되는 백분율 농도의 기초입니다. 
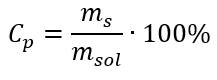백분율 농도에 대한 공식을 이전에 변환된 몰 농도에 대한 공식으로 대체하면 두 값 사이를 자유롭게 전환할 수 있는 관계를 얻을 수 있습니다. 
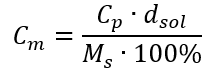공식의 유일한 제한은 적절한 단위를 사용하는 것이므로 모든 계산에서 고려하는 것이 좋습니다. 예 5. 백분율 농도가 C p = 98.0%이고 밀도가 d = 1.84 kg/dm 3 임을 알고 황산(VI)의 몰 농도를 계산합니다. 이것은 두 가지 방법을 사용하여 계산할 수 있습니다. 방법 1. 공식을 사용하지 않고 몇 단계로 1단계. 산의 1.00dm 3 질량 계산 
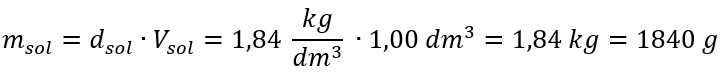2단계. 백분율 농도를 고려한 산의 질량 계산 
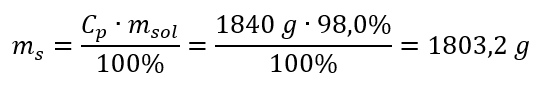3단계. 몰수 계산 
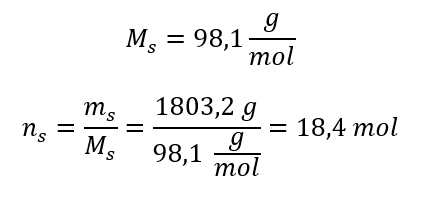4단계. 용액의 1dm3 당 물질의 몰수임을 알고 몰농도 계산 
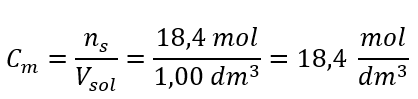방법 2. 백분율 농도와 몰 농도의 관계 이용 
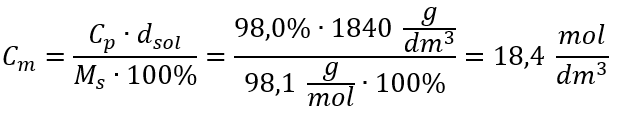답변: 이 산의 몰 농도는 18.4 mol/dm 3 입니다.
