전기 음성도는 분자 내의 특정 원자가 전자를 끌어당기는 경향을 반영하는 양입니다. 실제로 전자 밀도를 끌어당기는 것은 원자나 작용기의 능력입니다. 이 수량과 관련하여 가장 일반적으로 사용되는 척도는 Linus Pauling이 도입한 척도로, 채권의 대략적인 성격을 쉽게 계산할 수 있습니다.

전기음성도 특성
동핵 분자(예: H 2 및 O 2 )는 분자 궤도에서 동일한 계수 c A 및 c B를 가지며, 이는 파동 함수로 기록될 수 있습니다. Ψ +AB = c A Ψ A + c B Ψ B Ψ −AB = c A Ψ A − c B Ψ B 이 경우 오비탈은 분자 중심을 기준으로 모양이 대칭이고 전하가 그 안에 균등하게 대칭으로 분포되어 있는 것이 특징입니다. 그러나 또 다른 예는 이핵 분자로, 분자 중심에 대한 완전한 대칭뿐만 아니라 동일한 계수를 유지하는 것이 사실상 불가능합니다. 원자 궤도 Ψ B 의 에너지 준위가 원자 궤도 Ψ A 의 에너지 준위보다 낮을 때 관계가 발생하고 전자 확률 밀도의 최대값은 원자 B 쪽으로 이동합니다. 실제로 이로 인해 전자의 이동이 발생합니다. 즉, 원자 B를 향한 분극입니다. 예를 들어, 수소화리튬 분자 LiH에서 이러한 이동은 수소 원자를 향하는 반면, 불화수소 분자 HF에서는 불소 원자를 향합니다. 이는 수소 원자가 리튬보다 에너지 준위가 낮지만 불소보다 에너지 준위가 높다는 것을 의미합니다( 할로겐 에 대해 읽어보세요). 이러한 조건에서 두 분자의 원자 중 하나는 -δ로 표시된 음전하를 띠고 다른 하나는 양전하 +δ를 갖습니다. 이러한 분자의 일반식은 A +δ B -δ 입니다.
원자의 전하
앞서 언급한 전하 δ는 화학 결합 에 의해 결합된 원소에 따라 다른 값을 가질 수 있습니다. 값이 0이라는 것은 전자쌍의 전하가 대칭적으로 분포되어 있고 전자쌍이 에너지 준위가 낮은 원자 근처에 완전히 위치하여 두 전자가 해당 원자로 이동한다는 것을 의미합니다. 이것은 요소들 사이에 이온 결합을 생성합니다. 그러나 대부분의 화학 결합에는 부분 전하가 있어 공유 결합과 이온 결합 사이의 상태가 됩니다.
쌍극자 모멘트
쌍극자는 양극과 음극의 두 극이 구별될 수 있는 분자입니다. μ로 표시되는 쌍극자 모멘트는 전하 이동의 크기를 측정한 것입니다. 극 중 하나에 포함된 전하의 절대값(δ)과 이들 극으로부터의 거리(l)의 곱으로 정의됩니다. μ = δ·l 양전하(δ+)와 음전하( δ-)는 부분 전하라고 불리며 그 위치는 특정 원자에 기인하지만 실제로는 핵 주위에 전자가 존재할 확률이 더 높거나 낮을 뿐입니다. 이러한 현상은 때때로 산화 및 환원 과정과 혼동되지만, 원자에서 일어나는 변화와는 달리 원자가 이러한 전하를 띠더라도 다른 산화 상태로 이동하지 않으므로 원자 간 전자 교환이 없습니다. 그들을. 쌍극자 모멘트를 표현하는 SI 단위는 쿨롱미터(C·m)입니다. 그러나 계산에서는 CGS 시스템으로 작성된 단위인 데바이(D)가 가장 일반적으로 사용됩니다. 1디바이는 3.33564·10 -30 C·m 값에 해당합니다. 이론적으로 가능한 가장 큰 쌍극자 모멘트는 순수한 이온 결합을 갖는 분자의 특징입니다. 반면, 가장 작은 것은 결합이 순전히 공유 결합인 분자에서 발생합니다. 이 경우 쌍극자 모멘트는 0입니다. 그러나 대부분은 입자 특성이 다양한 중간 사례입니다.
할로겐 쌍극자 모멘트
특정 화합물에서 전기음성도와 쌍극자 모멘트 사이의 여러 관계를 쉽게 관찰할 수 있습니다. 풀 사이즈 테이블 1 할로겐화수소의 쌍극자 모멘트
| 화합물 | 실험적으로 결정된 쌍극자 모멘트 [ μ, D] | 본드 길이 [pm] | 원소 전하와 쌍극자 길이의 곱 [e ·l, D] | 이온성 문자 [ %]의 점유율 | 할로겐과 수소의 전기 음성도 차이 |
| HF | 1.98 | 92 | 4.42 | 45 | 1.9 |
| HCl | 1.08 | 128 | 6.15 | 18 | 0.9 |
| HBr | 0.79 | 143 | 6.87 | 12 | 0.7 |
| 안녕 | 0.38 | 162 | 7.78 | 5 | 0.4 |
비율 μ/(e·l’), 즉 이온 결합에 해당하는 쌍극자 모멘트에 대한 실제 쌍극자 모멘트는 완전 공유 결합으로부터의 편차를 측정할 수 있습니다. (μ/(e·l’))·100%형태의 이 관계의 곱은 결합의 이온 특성의 백분율을 나타냅니다. 쌍극자 모멘트는 결합의 극성뿐만 아니라 자유 전자쌍의 거동에도 영향을 받기 때문에 이는 대략적인 값일 뿐입니다. 전자 구름이 분자 외부로 이동할 수 있으며, 그 결과 쌍극자 모멘트를 결정하는 방정식에 추가 구성 요소가 포함됩니다. 암모니아 분자의 경우, 구름은 결합의 쌍극자 모멘트에 맞춰 방향을 지정하므로 결과적인 쌍극자 모멘트가 증가합니다. 대조적으로, 일산화탄소 분자의 경우 그 반대가 적용되는데, 구름이 반대 방향으로 향하고 결과적으로 쌍극자 모멘트가 감소합니다. 
전기음성도
이는 분자 내 특정 원자가 전자를 끌어당기는 경향을 반영하는 무차원 경험량입니다. 실제로 전자 밀도를 끌어당기는 것은 원자나 작용기의 능력입니다. 이 수량과 관련하여 가장 일반적으로 사용되는 척도는 Linus Pauling이 도입한 척도로, 채권의 대략적인 성격을 쉽게 계산할 수 있습니다. 과학자는 다음 방법을 사용하여 개별 원소의 전기음성도를 계산했습니다. D AA 와 D BB 는 두 원자 분자(A 2 , B 2 )의 결합 에너지라고 가정합니다. 분자에서 발생하는 결합 에너지를 D AB 로 지정합니다. 경험적으로, 이러한 결합이 이온 특성을 거의 또는 전혀 포함하지 않는 경우 D AB 값과 D AA 및 D BB 에너지 값의 기하 평균 간의 차이는 0과 같거나 0에 가까운 것으로 나타났습니다. AB 결합이 공유 결합 특성과 뚜렷한 편차가 있는 경우 이 차이는 양수 값을 가지며 이온 특성의 비율이 증가함에 따라 증가합니다. 결합에 관련된 두 원자의 전기음성도(x)의 차이는 다음 공식으로 표현됩니다. ![]() 따라서 폴링이 계산에서 불소의 전기음성도를 4.0으로 가정했다면 이후의 원소의 전기음성도를 계산하는 것이 가능합니다. 원소 A 원자의 x A 값과 계수 Δ’의 값을 알고 있으면 위 방정식을 사용하여 x B 값을 계산할 수 있습니다. 폴링 척도는 그 값이 할로겐화수소에 대해 결정된 값을 포함하는 표 1의 예에서 볼 수 있듯이 고려 중인 원자에 의해 형성된 결합의 쌍극자 모멘트 값과 대략 일치하는 방식으로 구성됩니다. . 위에서 설명한 척도 외에도 과학 문헌에는 다음과 같이 설명된 전기음성도를 포함하여 몇 가지가 더 설명되어 있습니다.
따라서 폴링이 계산에서 불소의 전기음성도를 4.0으로 가정했다면 이후의 원소의 전기음성도를 계산하는 것이 가능합니다. 원소 A 원자의 x A 값과 계수 Δ’의 값을 알고 있으면 위 방정식을 사용하여 x B 값을 계산할 수 있습니다. 폴링 척도는 그 값이 할로겐화수소에 대해 결정된 값을 포함하는 표 1의 예에서 볼 수 있듯이 고려 중인 원자에 의해 형성된 결합의 쌍극자 모멘트 값과 대략 일치하는 방식으로 구성됩니다. . 위에서 설명한 척도 외에도 과학 문헌에는 다음과 같이 설명된 전기음성도를 포함하여 몇 가지가 더 설명되어 있습니다.
- Mulliken은 원소의 전기음성도가 전자 친화력과 이온화 에너지의 합에 정비례한다고 가정했습니다. 전자 친화력은 중성 원자에 전자가 부착되어 방출되는 에너지의 양이고, 이온화 에너지는 중성 원자에서 전자를 분리하는 데 필요한 에너지의 양과 같습니다. 따라서 가장 높은 전기 음성도는 높은 전자 친화력과 높은 이온화 에너지를 나타내는 원자의 특징입니다.
- 원자핵(Z)이 원자가 전자에 작용하는 힘의 척도에 대한 전기음성도의 비례성을 가정한 Allred와 Rochow는 다음과 같이 기록했습니다.
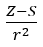 (r – 원자 반경, S – 스크리닝 상수). 그들의 이론에 따르면 원소의 전기음성도(x)는 다음 공식을 사용하여 계산할 수 있습니다.
(r – 원자 반경, S – 스크리닝 상수). 그들의 이론에 따르면 원소의 전기음성도(x)는 다음 공식을 사용하여 계산할 수 있습니다.
![]() 각 척도에서 수소의 전기음성도는 2.2 값에 가깝고 다른 값은 약간 다릅니다. Pauling, Mulliken, Allred 및 Rochow 척도에 따라 계산된 원소 원자의 전기음성도의 예가 아래 표 2에 나와 있습니다. 표 2 Pauling(P), Mulliken(M), Allred 및 Rochow(AR) 척도에서 예제 요소의 전기음성도
각 척도에서 수소의 전기음성도는 2.2 값에 가깝고 다른 값은 약간 다릅니다. Pauling, Mulliken, Allred 및 Rochow 척도에 따라 계산된 원소 원자의 전기음성도의 예가 아래 표 2에 나와 있습니다. 표 2 Pauling(P), Mulliken(M), Allred 및 Rochow(AR) 척도에서 예제 요소의 전기음성도
| 원자 | 피 | 중 | 아칸소 |
| 에프 | 3.98 | 3.90 | 4.10 |
| 영형 | 3.44 | 3.04 | 3.50 |
| N | 3.04 | 2.28 | 3.07 |
| Cl | 3.16 | 2.95 | 2.83 |
| 씨 | 2.55 | 1.75 | 2.50 |
| 시간 | 2.20 | 2.21 | 2.20 |
| 시 | 1.90 | 2.25 | 1.74 |
| 에프 | 0.82 | 0.77 | 0.91 |
| Rb | 0.82 | 0.50 | 0.89 |
| CS | 0.79 | – | 0.86 |
| 정말로 | 0.70 | – | 0.86 |
세 가지 방법의 계산 불일치에도 불구하고 불소는 각 규모에서 가장 높은 전기 음성도를 가지며 산소, 질소 및 염소가 그 뒤를 따릅니다. 가장 낮은 값은 프랑슘, 세슘, 루비듐 및 칼륨에 대해 결정되었습니다. 일반적으로 비금속인 원소의 전기음성도는 2보다 크고, 일반적인 금속의 전기음성도는 2 미만입니다. 표준 값은 앞서 언급한 수소의 전기음성도 약 2.2입니다. 
주기율표의 전기음성도
다른 많은 특성과 마찬가지로 전기음성도는 주기율표의 화학 원소 배열에도 반영됩니다. 그룹에서는 껍질의 수와 금속성이 증가함에 따라 전기 음성도가 감소하므로 프랑슘에서 수소 방향으로 증가합니다. 시간이 지남에 따라 존재하는 원자가 전자가 증가하고 비금속 특성이 감소함에 따라 전기 음성도가 증가하므로 금속에서 희가스 로 변합니다.
전기 음성도 및 결합 유형 – 요약
화학 결합을 형성하는 원소의 전기 음성도의 개별 값을 알면 그 성질을 추론할 수 있습니다. 차이가 0.0에서 0.4 사이이면 결합은 공유 결합입니다. 차이가 0.4와 1.7 사이이면 결합은 극성 공유 결합입니다. 원소의 전기음성도 차이가 1.7보다 크면 이온 결합을 의미합니다.
