Energia chemických reakcií

Systém a prostredie chemickej reakcie

Pre správnu interpretáciu chemickej reakcie z hľadiska energie potrebujeme mať určité znalosti o nasledujúcich veciach:

1. Systém: oddelená oblasť hmoty s jasnými hranicami. Typ systému je dôležitý: je otvorený, ak reakcia zahŕňa výmenu energie a hmoty, uzavretý, ak reakcia zahŕňa iba výmenu energie, alebo izolovaný, ak nedochádza k výmene energie ani hmoty.
2. Prostredie: čokoľvek, čo nie je súčasťou systému, ale nachádza sa v blízkosti.
3. Systémové komponenty: všetky látky, ktoré sa nachádzajú v analyzovanom systéme a majú svoje charakteristické chemické vlastnosti.

Energia chemických väzieb

Energetický efekt, ktorý charakterizuje akúkoľvek chemickú reakciu, je výsledkom zmien vyskytujúcich sa pri prerušovaní a vytváraní nových väzieb medzi atómami. Faktom je, že každé prerušenie chemickej väzby je vnútorne spojené s absorpciou primeraného množstva energie, pričom vznik novej väzby spôsobuje produkciu energie. Uvoľňovanie energie do okolia môže mať rôzne účinky: teplo, svetlo, práca alebo elektrina. Každý z týchto procesov je komponentným faktorom, ktorý ovplyvňuje všeobecnú zmenu vnútornej energie systému, v ktorom prebieha reakcia. Je dôležité, že bez ohľadu na to, či reagencie musia počas transformácie odobrať alebo odovzdať energiu, na spustenie celého procesu je vždy potrebné určité množstvo energie.

Prvý zákon termodynamiky

Prvým dôležitým pravidlom týkajúcim sa energie chemických reakcií je vzťah formulovaný v prvom termodynamickom zákone, ktorý hovorí, že vnútorná energia systému, ktorý si iba vymieňa energiu s okolím (uzavretý systém), sa môže premeniť iba na teplo alebo prácu. To sa odráža v Helmholtzovej rovnici: ∆U = Q + W Kde ΔU znamená zmenu vnútornej energie, Q znamená teplo a W znamená prácu. Zo vzorca si môžeme všimnúť, že vnútorná energia izolovaného systému, teda takého, ktorý si nevymieňa energiu ani hmotu s okolím, je konštantná. Zložkami vnútornej energie sú všetky kinetické energie atómov, iónov, molekúl, elektrónov a zložiek atómového jadra, ktoré sa práve nachádzajú v reakčnom systéme, ako aj energie ich interakcií, teda energie chemických väzieb, interakcií. medzi poplatkami a tak ďalej. Upozorňujeme, že vnútorná energia neobsahuje kinetickú ani potenciálnu energiu systému ako celku. Súčet kinetických a potenciálnych energií systému ako celku a vnútornej energie je celková energia systému (E).

Systémová entalpia (H)

Ide o ďalší dôležitý pojem súvisiaci s energiou chemických reakcií, čo v praxi znamená súčet vnútornej energie systému a súčinu jeho tlaku a objemu. V kvalitatívnom vyjadrení je to energia potrebná na výrobu systému vo vákuu (U), zvýšená o prácu, teda podiel tlaku a objemu (pV), ktorú musí systém vykonať proti vonkajším silám, aby sa dosiahol objem odlišný od nula. Vzťah definujúci entalpiu systému je vyjadrený takto: H = U + pV Reakcia prebiehajúca v takomto systéme spôsobí nekonečne malú zmenu entalpie: dH = dU + dpV + pdV Ak sú reakčné podmienky izobarické, tak ak tlak počas proces sa nemení, druhú časť možno vynechať, pretože dpV=0. Po dosadení diferenciálov za určité prírastky a po nahradení výrazu týkajúceho sa zmeny vnútornej energie systému dostaneme nasledujúci vzťah: ∆H = Q + W + p∆V Za predpokladu, že analyzovaný proces vykonáva objemovú prácu pri konštantnom tlaku. , potom W = -pΔV a následne: ∆H = Q – p∆V + p∆V Z rovnice vyplýva, že ak reakcia prebieha pri konštantnom tlaku, potom sa zmena entalpie systému rovná teplu: ∆H = Q

Energetické schopnosti reakcie

Na základe vyššie odvodeného vzorca, ktorý naznačuje, že zmena entalpie systému sa môže rovnať reakčnému teplu, sú procesy klasifikované podľa tepelných premien. Z hľadiska smeru toku energie delíme chemické reakcie na:

1. Exotermické reakcie, čo sú také reakcie, pri ktorých môžeme pozorovať emisiu energie, napríklad vo forme tepla, do okolia systému. Stáva sa to vtedy, keď súčet entalpií produktov je nižší ako súčet entalpií substrátov, teda keď ΔH<0.
2. Endotermické reakcie, teda také chemické reakcie, ktoré spôsobujú absorpciu energie z prostredia. Podmienkou takejto reakcie je dodanie primeraného množstva tejto energie. Platí to pre všetky transformácie, pri ktorých je celková entalpia produktov vyššia ako celková entalpia substrátov, teda ΔH>0.

Zápisy chemických reakcií

Vzhľadom na chemické reakcie spolu s ich potrebou energie a distribúciou sú ich špecifické tepelné účinky zahrnuté v zápise chemickej rovnice. Pri exotermických reakciách je absolútna hodnota existujúceho tepelného efektu uvedená na strane produktu. Naopak, keď sa zaznamenáva endotermická reakcia, absolútna hodnota absorbovanej energie je zaznamenaná na strane substrátu. Uvediem príklad:

1. Exotermická reakcia:
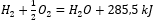
2. Endotermická reakcia: _2H3P04 + _3Mg (OH) ₂ + 407 kJ = _Mg3 (P04 _{) 2 +} 6H20

Ďalším spôsobom je zaznamenať si chemickú rovnicu spolu s hodnotou energetického efektu uvedenou stranou. V tomto prípade je hodnota predstavujúca energiu exoenergickej reakcie záporná, zatiaľ čo pre endoenergickú reakciu je kladná. Napríklad:

1. Exoenergická reakcia: Fe + S → FeS ∆H= -95,2 kJ/mol
2. Endoenergická reakcia: FeS → Fe + S ∆H= 95,2 kJ/mol

Hessov zákon

Tvorí základ pre termochemické výpočty a uvádza, že tepelný efekt je vždy rovnaký bez ohľadu na spôsob, akým sa reakcia uskutočňuje. To nám umožňuje vypočítať štandardnú entalpiu reakcie (Δ _r H ^ϴ ), za predpokladu použitia štandardných podmienok, tj tlaku 10 ⁵ Pa a akejkoľvek teploty. Keďže entalpia je funkciou skupenstva, jej variabilita závisí len od dvoch hodnôt: v počiatočnom a koncovom stave, ktorý pri chemickej reakcii predstavuje stav substrátov a stav produktov. Hessov zákon je vyjadrený rovnicou, ktorá obsahuje stechiometrické koeficienty (v) a štandardné molárne entalpie tvorby (Δ _f H ^ϴ ):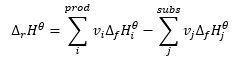

Štandardná molárna entalpia tvorby

Je to entalpia získaná vytvorením 1 mólu konkrétnej chemickej zlúčeniny z prvkov v ich základnom stave. Základný stav je najodolnejší variant prvku v špecifických podmienkach. Uvediem príklad, grafit je najodolnejší variant uhlíka pri 25 ^o C a 10 ⁵ Pa. Naopak, pri vysokej teplote a tlaku je stabilnou formou uhlíka diamant. Pre každý reaktant, ktorý sa zúčastňuje reakcie vo svojom základnom stave, je hodnota štandardnej molárnej entalpie tvorby nula. Zvyčajne ide o jednotlivé atómy vzácnych plynov alebo o najodolnejšie varianty iných plynov v špecifických podmienkach. Pre štandardný tlak (10 ⁵ Pa) a teplotu (normálne 25 ^o C) sú hodnoty štandardných molárnych entalpií tvorby zlúčenín zhrnuté v chemických tabuľkách. Jednotkou tejto hodnoty je . Hessov zákon aplikovaný na chemické reakcie znamená, že hodnota entalpie reakcie je nezávislá od počtu medzireakcií. Jedinou kľúčovou informáciou je, že na získanie konkrétnych produktov sa používajú konkrétne substráty.

Syntéza oxidu uhličitého

Syntéza oxidu uhličitého sa môže uskutočniť rôznymi spôsobmi, ale podľa Hessovho zákona každý z nich vedie k rovnakej hodnote zmien štandardných entalpií.

1. Priama syntéza
2. Syntéza oxidu uhlíka (II) + oxidácia zlúčeniny na oxid uhličitý (IV).

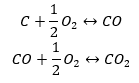Keď z tabuľky odčítame hodnoty štandardných entalpií tvorby zlúčenín a dosadíme ich do chemických rovníc, uvidíme, že entalpia pre každú metódu je rovnaká: -393,5 kJ/mol.

Kirchhoffov zákon

Umožňuje nám transformovať výpočty na výpočet štandardnej entalpie reakcie pre určitú teplotu, ak poznáme jej hodnotu pri inej teplote. Poznáme aj vzťahy medzi molárnym teplom všetkých reaktantov a teplotou. Zákon možno použiť, pretože zmena entalpie reakcie závisí od podmienok, v ktorých bola stanovená: mení sa spolu s meniacou sa teplotou a tlakom. Odvodenie vzorca by sa malo začať definovaním tepelnej kapacity, čo je pomer dodaného tepla k nárastu teploty: Za predpokladu izotermických podmienok môžeme urobiť nasledujúcu transformáciu: Integrácia výslednej rovnice a prepočet tepelnej kapacity na časť predstavujúcu zmenu štandardnej tepelnej kapacity sa odráža v rovnici, ktorú poskytuje Kirchhoffov zákon: 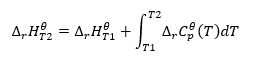Pre štandardné podmienky je zmena tepelnej kapacity reakcie definovaná rovnicou s v-premennými, ktoré sú stechiometrickými faktormi a , čo predstavuje štandardné molárne teplo daného reaktantu. Keď je teplotný rozdiel malý (do 100 K), predpokladá sa, že hodnota štandardného molárneho tepla reaktantu je v určitom rozsahu konštantná. Potom môžeme použiť zjednodušenú formu Kirchhoffovho zákona za predpokladu, že tepelné kapacity reaktantov nezávisia od teploty, ale od konštantného tlaku, :