Energin i kemiska reaktioner är ett av de viktiga element som gör att vi kan förstå de omvandlingar som sker i en kemisk reaktion. Vid en sådan omvandling framställs kemiska föreningar med en struktur och kemisk sammansättning som skiljer sig från de råvaror de är gjorda av. Under en kemisk reaktion bryts de bindningar som finns mellan atomerna i de molekyler som används som reaktanter och nya bindningar bildas – som finns i produkterna.
Systemet och miljön för en kemisk reaktion
För en korrekt tolkning av en kemisk reaktion i termer av energi behöver vi ha viss kunskap om följande:
- System: ett avskilt område av materia med tydliga gränser. Typen av system är viktig: det är öppet om reaktionen innebär utbyte av energi och materia, stängt om reaktionen endast innebär utbyte av energi, eller isolerat om varken energi eller materia byts ut.
- Miljö: allt som inte ingår i systemet men som finns i närheten.
- Systemkomponenter: alla ämnen som finns i det analyserade systemet och har sina karakteristiska kemiska egenskaper.
Energin hos kemiska bindningar
Den energieffekt som kännetecknar varje kemisk reaktion är resultatet av förändringar som sker samtidigt som de bryts av och producerar nya bindningar mellan atomer. Faktum är att varje brott av en kemisk bindning är naturligt kopplad till absorptionen av en lämplig mängd energi, medan bildandet av en ny bindning orsakar produktion av energi. Utsläpp av energi till miljön kan ha olika effekter: värme, ljus, arbete eller el. Var och en av dessa processer är en komponentfaktor som påverkar den allmänna förändringen i den inre energin i systemet där reaktionen äger rum. Det är viktigt att, oavsett om reagensen måste dra eller avstå från energi under omvandlingen, det alltid krävs en viss mängd energi för att få igång hela processen.
Termodynamikens första lag
Den första viktiga regeln angående energin i kemiska reaktioner är förhållandet formulerat i termodynamikens första lag, som säger att den inre energin i ett system som endast utbyter energi med omgivningen (ett slutet system) bara kan omvandlas till värme eller arbete. Detta återspeglas i Helmholtz-ekvationen: ∆U = Q + W Där ΔU betecknar förändringen i intern energi, Q betecknar värme och W betecknar arbete. Vi kan märka från formeln att den inre energin i ett isolerat system, dvs ett som inte byter energi eller massa med omgivningen, är konstant. Komponenter i den inre energin är alla kinetiska energier av atomer, joner, molekyler, elektroner och komponenter i atomkärnan, som för närvarande finns i reaktionssystemet, såväl som energierna för deras interaktioner, det vill säga energierna av kemiska bindningar, interaktioner mellan avgifter och så vidare. Observera att den inre energin inte innehåller kinetisk eller potentiell energi för systemet som helhet. Summan av kinetiska och potentiella energier för systemet som helhet och den inre energin är systemets totala energi (E).
Systementalpi (H)
Detta är ett annat viktigt begrepp relaterat till energin från kemiska reaktioner, vilket i praktiken betyder summan av systemets inre energi och produkten av dess tryck och volym. I kvalitativa termer är det energin som krävs för att producera ett system i vakuum (U), ökat med arbete, dvs kvoten av tryck och volym (pV), som systemet måste utföra mot yttre krafter för att uppnå en volym som skiljer sig från noll. Relationen som definierar ett systems entalpi uttrycks enligt följande: H = U + pV En reaktion som sker i ett sådant system orsakar en oändligt liten förändring i entalpi: dH = dU + dpV + pdV Om reaktionsförhållandena är isobariska, så om trycket under processen ändras inte, den andra delen kan utelämnas, eftersom dpV=0. Efter att ha ersatt differentialer med bestämda inkrement och efter att ha ersatt uttrycket som hänvisar till förändringen av systemets interna energi, får vi följande samband: ∆H = Q + W + p∆V Om vi antar att den analyserade processen utför ett volymetriskt arbete vid ett konstant tryck , då W = -pΔV, och följaktligen: ∆H = Q – p∆V + p∆V Det följer av ekvationen att om reaktionen sker vid ett konstant tryck, så är förändringen i systemets entalpi lika med värmen: ∆H = Q
Energetiska förmågor hos en reaktion
Baserat på formeln härledd ovan, som indikerar att förändringen i systemets entalpi kan vara lika med reaktionsvärmet, klassificeras processer enligt termiska transformationer. När det gäller energiflödets riktning delar vi in kemiska reaktioner i:
- Exotermiska reaktioner, som är sådana reaktioner där vi kan observera utsläpp av energi, till exempel i form av värme, till systemets miljö. Detta händer när summan av entalpier för produkterna är lägre än summan av entalpier för substraten, så när ΔH<0.
- Endotermiska reaktioner, så sådana kemiska reaktioner som orsakar absorption av energi från miljön. En förutsättning för en sådan reaktion är att leverera en lämplig mängd av den energin. Detta gäller alla transformationer för vilka produkternas totala entalpi är högre än substratens totala entalpi, alltså ΔH>0.
Noteringar av kemiska reaktioner
Med tanke på kemiska reaktioner tillsammans med deras energibehov och distribution, är deras specifika värmeeffekter inkluderade i notationen av en kemisk ekvation. För exoterma reaktioner noteras det absoluta värdet av den befintliga värmeeffekten på produktsidan. Omvänt, när man noterar en endoterm reaktion, noteras det absoluta värdet av den absorberade energin på substratsidan. För att ge ett exempel:
- Exoterm reaktion:
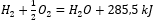
- Endoterm reaktion: 2H 3 PO 4 + 3 Mg(OH) 2 + 407 kJ = Mg 3 (PO 4 ) 2 + 6H 2 O
Ett annat sätt är att notera en kemisk ekvation tillsammans med energieffektvärdet som ges åt sidan. I detta fall är värdet som representerar energin för en exoenergisk reaktion negativt, medan det är positivt för en endoenergisk reaktion. Till exempel:
- Exoenergisk reaktion: Fe + S → FeS ∆H= -95,2 kJ/mol
- Endoenergisk reaktion: FeS → Fe + S ∆H= 95,2 kJ/mol
Hess lag
Den utgör en grund för termokemiska beräkningar, som säger att värmeeffekten alltid är densamma oavsett hur reaktionen utförs. Detta tillåter oss att beräkna standardentalpin för en reaktion (Δ r H ϴ ), under antagande av användningen av standardbetingelser, det vill säga ett tryck på 10 5 Pa och vilken temperatur som helst. Eftersom entalpi är en funktion av tillstånd beror dess variabilitet på endast två värden: i det initiala och slutliga tillståndet, vilket i en kemisk reaktion representerar tillståndet hos substrat respektive produkternas tillstånd. Hess lag uttrycks av en ekvation som innehåller stekiometriska koefficienter (v) och standard molära entalpier för bildning (Δ f H ϴ ):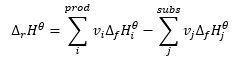 
Standard molär entalpi för bildning
Det är en entalpi som erhålls genom att bilda 1 mol av en viss kemisk förening från grundämnen i deras grundläggande tillstånd. Grundtillståndet är den mest hållbara varianten av elementet under specifika förhållanden. För att ge ett exempel är grafit den mest hållbara varianten av kol vid 25 o C och 10 5 Pa. Omvänt, vid hög temperatur och högt tryck är en stabil form av kol diamant. För varje reaktant som deltar i en reaktion i dess grundtillstånd är värdet på standard molär bildningsentalpi noll. Vanligtvis är dessa individuella atomer av ädelgaser eller de mest hållbara varianterna av andra gaser under specifika förhållanden. För ett standardtryck (10 5 Pa) och temperatur (normalt 25 o C), är värdena för standard molära entalpier för bildning av föreningar samlade i kemiska tabeller. Enheten för det värdet är . Hess lag tillämpad på kemiska reaktioner innebär att reaktionens entalpivärde är oberoende av antalet mellanreaktioner. Den enda nyckelinformationen är att särskilda substrat används för att få fram särskilda produkter.
Syntesen av koldioxid
Syntesen av koldioxid kan utföras på olika sätt, men enligt Hess lag leder var och en av dem till samma värde av förändringar i standardentalpier.
- Direkt syntes
- Syntesen av kol(II)oxid + oxidation av föreningen till kol(IV)oxid
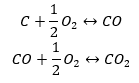När vi läser ut värdena för standardentalpier för bildning av föreningarna från tabellen och ersätter dem i de kemiska ekvationerna, kommer vi att se att entalpin för varje metod är densamma: -393,5 kJ/mol.
Kirchhoffs lag
Det gör det möjligt för oss att transformera beräkningarna för att beräkna standardentalpin för en reaktion för en viss temperatur, om vi vet dess värde vid en annan temperatur. Vi känner också till sambanden mellan molvärmen för alla reaktanter och temperaturen. Lagen kan tillämpas, eftersom förändringen i reaktionens entalpi beror på de förhållanden under vilka den bestämdes: den varierar tillsammans med förändrad temperatur och tryck. Härledningen av formeln bör startas genom att definiera den termiska kapaciteten, det vill säga förhållandet mellan tillförd värme och temperaturökningen: 
Om vi antar isotermiska förhållanden kan vi göra följande transformation: 
Integration av den resulterande ekvationen och omvandlingen av termisk kapacitet till den del som representerar förändringen i standardvärmekapacitet återspeglas av ekvationen som tillhandahålls av Kirchhoffs lag: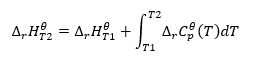 
För standardförhållanden definieras förändringen i en reaktions termiska kapacitet av ekvationen med v-variabler, som är stekiometriska faktorer, och , som representerar standardmolarvärmen för en given reaktant. När temperaturskillnaden är liten (upp till 100K) antas värdet på reaktantens standardmolära värme vara konstant inom ett visst område. Sedan kan vi använda den förenklade formen av Kirchhoffs lag, förutsatt att reaktanternas termiska kapacitet inte beror på temperaturen utan på konstant tryck, : 
